Тест на определение нормальности: Тест на определение степени вашей нормальности

Содержание

Как проверить нормальность в SPSS

Многие статистические тесты требуют, чтобы одна или несколько переменных были нормально распределены, чтобы результаты теста были надежными.

В этом руководстве объясняются два разных метода, которые можно использовать для проверки нормальности переменных в SPSS.

Каждый метод будет использовать следующий набор данных, который показывает среднее количество очков за игру, набранных 20 разными баскетболистами:

Метод 1: гистограммы

Один из способов проверить, нормально ли распределена переменная, — создать гистограмму для просмотра распределения переменной. Если переменная распределена нормально, гистограмма должна принять форму «колокола» с большим количеством значений, расположенных ближе к центру, и меньшим количеством значений, расположенных на хвостах.

Чтобы создать гистограмму для этого набора данных баскетбола, мы можем щелкнуть вкладку « Графики », а затем « Построитель диаграмм ».

В появившемся окне выберите Histogram в списке Choose from и перетащите его в окно редактирования. Затем перетащите переменные точки на ось x:

После того, как вы нажмете OK , появится следующая гистограмма:

Мы видим, что переменные очки распределены не совсем нормально, но они примерно соответствуют форме колокола, при этом большинство игроков набирают от 10 до 20 очков за игру, и меньшее количество игроков набирает больше, чем это количество.

Хотя это не формальный способ проверки нормальности, он дает нам быстрый способ визуализировать распределение переменной и дает нам приблизительное представление о том, является ли распределение колоколообразным.

Метод 2: формальные статистические тесты

Мы также можем использовать формальные статистические тесты, чтобы определить, следует ли переменная нормальному распределению. SPSS предлагает следующие тесты на нормальность:

Тест Шапиро-Уилка
Тест Колмогорова-Смирнова

Нулевая гипотеза для каждого теста состоит в том, что данная переменная имеет нормальное распределение. Если p-значение теста меньше некоторого уровня значимости (обычный выбор включает 0,01, 0,05 и 0,10), то мы можем отклонить нулевую гипотезу и сделать вывод, что имеется достаточно доказательств того, что переменная не имеет нормального распределения.

Чтобы выполнить оба этих теста в SPSS одновременно, щелкните вкладку « Анализ », затем « Описательная статистика », затемИсследуйте :

В новом появившемся окне перетащите переменные точки в поле с надписью Зависимый список. Затем щелкните Графики и убедитесь, что установлен флажок рядом с Графики нормальности с тестами.Затем нажмите «Продолжить».Затем нажмите ОК .

После того, как вы нажмете OK , результаты тестов нормальности будут показаны в следующем поле:

Показаны статистика теста и соответствующее значение p для каждого теста:

Тест Колмогорова-Смирнова:

Статистика теста: 0,113
p-значение: 0,200

Тест Шапиро-Уилка:

Статистика теста: 0,967
p-значение: 0,699

Значения p для обоих тестов не менее 0,05, что означает, что у нас нет достаточных доказательств, чтобы сказать, что переменные баллы не распределены нормально.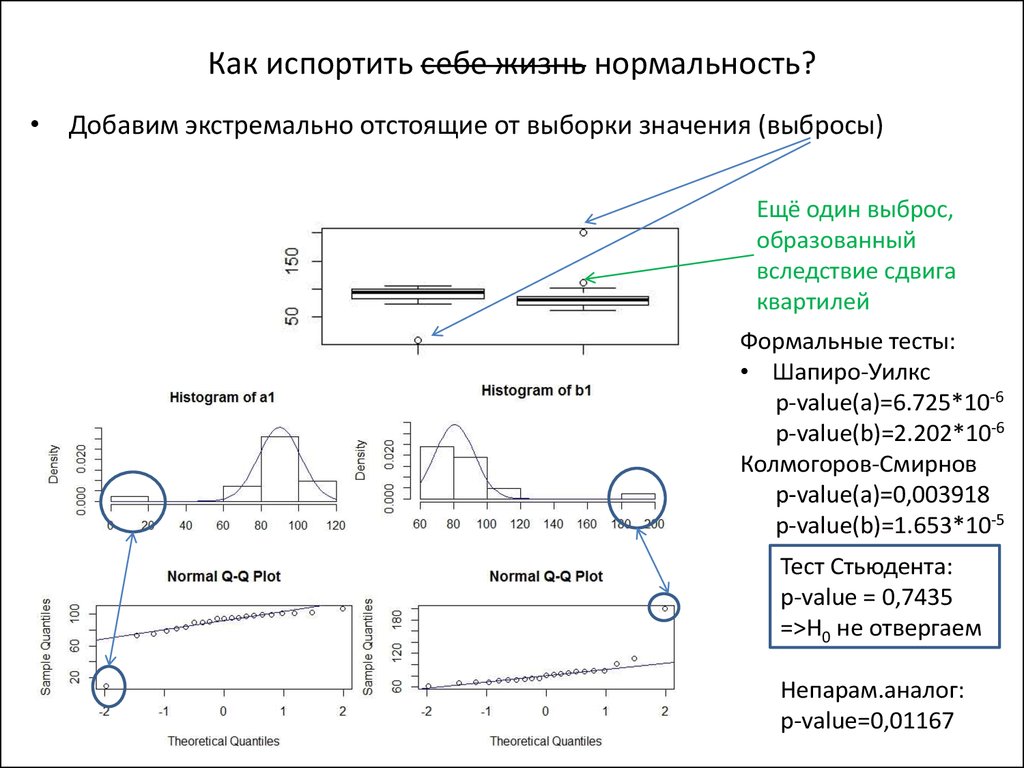

Если бы мы захотели выполнить некоторый статистический тест, предполагающий, что переменные распределены нормально, мы бы знали, что переменные точки удовлетворяют этому предположению.

Тест на психопатию

Tests
Types
Articles
News
Members
Search

Этот тест также доступен на таких языках：

Оценочный лист психопатии Хаэра (PCL-R) — это один из самых известных опросников, которые используют для определения уровня психопатии. Обычно, его используют, чтобы обнаружить психопатические или антисоциальные наклонности личности. Психопаты безжалостно манипулируют другими, используя харизму, обманы и жестокость для достижения своих целей. Этот тест опирается на оценочный лист психопатии Хаэра, однако также использует факторные анализы.

Есть ли у Вас или Ваших знакомых черты психопатии? Для каждого следующего утверждения укажите, насколько оно касается Вас или выбранного Вами человека.

Вопрос 1 из 20

Этот человек часто обманывал, лгал и манипулировал людьми.

Не касается. Частично касается / не знаю. Касается.

ПРОДОЛЖИТЬ НАЗАД

Тест IDR-PCT © является собственностью IDR Labs International. Первичное исследование принадлежит советнику ФБР и уголовному психологу Роберту Д. Хаэру. Тест IDR-PCT использует исследования Хаэра, однако этот тест не имеет непосредственного отношения к данному исследователю и не является идентичным с оценочным листом психопатии Хаэра (PCL-R). Этот тест никоим образом не связан с Робертом Хаэром, его коллегами или соответствующими учреждениями. Этот тест не нарушает никаких прав собственности.

Оценочный лист психопатии широко используется для выявления признаков психопатии. Опросник не охватывает все возможные типы психопатии и не предназначен для респондентов, которые пытаются обойти систему и выйти за пределы человеческой психологии. Вопреки распространенному мнению оценочный лист психопатии — это не единственный метод выявления признаков психопатии. Согласно другому теоретическому источнику, который используется в таких психиатрических пособиях, как диагностическое и статистическое руководство по психических расстройствах, результаты оценочного листа психопатии во многом совпадают с нарциссическим, эмоционально нестабильным и антисоциальным типами личности.

Чтобы узнать больше об этих типах личности, пройдите, пожалуйста, наш Тест на определение расстройства личности.

Хотя этот тест предназначен для выявления признаков психопатии, его не следует путать с другими похожими тестами, которые разработаны альтернативными организациями. Однако все тесты этого типа созданы с целью определения уровня психопатии личности согласно исследованиям Западного мира. Тест IDR-PCT © является собственностью IDR Labs International. Первичное исследование принадлежит криминальному психологу Роберту Д. Хаэру. Разработчики этого бесплатного теста являются дипломированными специалистами, которые имели опыт работы с многочисленными личностными тестами, а также работали на профессиональном уровне с тестированиями типологии личности. Результаты нашего онлайн-теста на психопатию предоставляются «как есть» и не должны толковаться как предоставление профессиональной или сертифицированной консультации любого рода. Для получения дополнительной информации о нашем онлайн-тесте ознакомьтесь, пожалуйста, с нашими Условиями предоставления услуг.

Тестирование на нормальность с помощью SPSS Statistics при наличии только одной независимой переменной.

Введение

Оценка нормальности данных является обязательным условием для многих статистических тестов, поскольку нормальные данные являются основным предположением в параметрическом тестировании. Существует два основных метода оценки нормальности: графически и численно.

Это краткое руководство поможет вам определить, являются ли ваши данные нормальными и, следовательно, соответствует ли это предположение вашим данным для статистических тестов. Подходы можно разделить на две основные темы: опора на статистические тесты или визуальный осмотр. Преимущество статистических тестов состоит в том, что они дают объективную оценку нормальности, но их недостаток заключается в том, что иногда они недостаточно чувствительны при малых размерах выборки или чрезмерно чувствительны к большим размерам выборки. Таким образом, некоторые статистики предпочитают использовать свой опыт для субъективного суждения о данных, полученных на графиках/графиках. Преимущество графической интерпретации заключается в том, что она позволяет здраво оценить нормальность в ситуациях, когда численные тесты могут быть слишком чувствительными или недостаточными, но графические методы не обладают объективностью. Если у вас нет большого опыта графической интерпретации нормальности, вероятно, лучше полагаться на численные методы.

Если вы хотите ознакомиться с процедурой проверки на нормальность в SPSS Statistics для конкретного статистического теста, который вы используете для анализа данных, мы предоставляем исчерпывающие руководства в нашем расширенном содержании. Для каждого статистического теста, где вам нужно проверить нормальность, мы покажем вам, шаг за шагом, процедуру в SPSS Statistics, а также как действовать в ситуациях, когда ваши данные не соответствуют предположению о нормальности (например, когда вы можете попробуйте «преобразовать» ваши данные, чтобы сделать их «нормальными»; мы также покажем вам, как это сделать с помощью SPSS Statistics). Вы можете узнать о нашем расширенном контенте в целом в разделе «Функции»:

Обзор страницы или как мы помогаем с предположениями на нашей странице Возможности: предположения. Однако в этом кратком руководстве мы познакомим вас с основами проверки нормальности в SPSS Statistics.

Статистика SPSS

Методы оценки нормальности

SPSS Statistics позволяет протестировать все эти процедуры с помощью команды Explore… . Команду Исследовать… можно использовать изолированно, если вы проверяете нормальность в одной группе или разбиваете набор данных на одну или несколько групп. Например, если у вас есть группа участников и вам нужно знать, нормально ли распределен их рост, все можно сделать в пределах Исследовать… команда. Если вы разделите свою группу на мужчин и женщин (т. е. у вас есть категориальная независимая переменная), вы можете проверить нормальность роста как в мужской группе, так и в женской группе, используя только команду Исследовать.

.. . Это применимо, даже если у вас более двух групп. Однако, если у вас есть 2 или более категориальных независимых переменных, одной команды Исследовать… недостаточно, и вам также придется использовать команду Разделить файл… .

Примечание. Нижеследующие процедуры идентичны для SPSS Statistics версий 17–28 , а также для подписной версии SPSS Statistics, где версия 28 и подписная версия являются последними версиями статистики SPSS. Однако в версии 27 и подписной версии SPSS Statistics представила новый вид своего интерфейса под названием « SPSS Light 9».0010», заменив прежний вид версий 26 и более ранних версий , который назывался «

SPSS Standard ». SPSS Statistics), следующие изображения будут светло-серыми, а не синими. Однако процедуры идентичны .
SPSS Statistics
Процедура для отсутствия или одной группирующей переменной
Следующий пример взят из нашего руководства по выполнению однофакторного дисперсионного анализа в SPSS Statistics.
Щелкните A nalyze > D e scriptive Statistics > E explore… в верхнем меню, как показано ниже:
Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.
Вам будет представлено диалоговое окно Explore , как показано ниже:
Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.
Перенесите переменную, которую необходимо проверить на нормальность, в зависимое поле D List: либо перетаскиванием, либо с помощью кнопки. В этом примере мы переносим переменную Time в зависимое поле
D List:. Затем вам будет представлен следующий экран:
Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.
[Необязательно] Если вам нужно установить, нормально ли распределена ваша переменная для каждого уровня вашей независимой переменной, вам нужно добавить свою независимую переменную в поле Список акторов F : перетаскиванием или с помощью кнопки . В этом примере мы передаем переменную Course в поле списка акторов F . Вам будет представлен следующий экран:
Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.
Нажмите на кнопку. Вам будет представлено диалоговое окно Explore: Statistics , как показано ниже:
Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.
Оставьте вышеуказанные параметры без изменений и нажмите на кнопку.

Нажмите на кнопку. Измените параметры, чтобы отобразился следующий экран:
Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.
Нажмите на кнопку.
Нажмите на кнопку.
SPSS Statistics
Вывод

С помощью этой процедуры SPSS Statistics выводит множество таблиц и графиков. Одна из причин этого заключается в том, что команда Исследовать… используется не только для проверки нормальности, но и для описания данных различными способами. При тестировании на нормальность нас в основном интересует 9Таблица 0009 Tests of Normal и Normal Q-Q Plots , наши численные и графические методы проверки нормальности данных соответственно.

Тест нормальности Шапиро-Уилка

Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.

В приведенной выше таблице представлены результаты двух хорошо известных тестов нормальности, а именно критерия Колмогорова-Смирнова и критерия Шапиро-Уилка. Критерий Шапиро-Уилка больше подходит для небольших выборок (< 50 образцов), но также может работать с размерами выборок до 2000. По этой причине мы будем использовать критерий Шапиро-Уилка в качестве нашего численного средства оценки нормальности.

Из приведенной выше таблицы видно, что для групп курсов «Начинающий», «Средний» и «Продвинутый» зависимая переменная «Время» имеет нормальное распределение. Откуда нам это знать? Если Sig. значение теста Шапиро-Уилка больше 0,05, данные в норме. Если он ниже 0,05, данные значительно отклоняются от нормального распределения.

Если вам нужно использовать значения асимметрии и эксцесса для определения нормальности, а не тест Шапиро-Уилка, вы найдете их в нашем расширенном руководстве по тестированию на нормальность. Вы можете узнать больше о нашем расширенном контенте в наших возможностях: Обзор стр.

Нормальный график Q-Q

Для графического определения нормальности можно использовать выходные данные нормального графика Q-Q. Если данные распределены нормально, точки данных будут близки к диагональной линии. Если точки данных отклоняются от линии очевидным нелинейным образом, данные не распределены нормально. Как видно из нормального графика Q-Q ниже, данные распределены нормально. Если вы вообще не уверены в том, что сможете правильно интерпретировать график, полагайтесь на численные методы, потому что может потребоваться немало опыта, чтобы правильно оценить нормальность данных на основе графиков.

Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.

Если вам нужно знать, как выглядят нормальные графики Q-Q, когда распределения не являются нормальными (например, с отрицательным перекосом), вы найдете их в нашем расширенном руководстве по тестированию на нормальность. Вы можете узнать больше о расширенном контенте на нашей странице Возможности: Обзор .

« предыдущая

Выберите подходящий тест нормальности | by Javier Fernandez

Критерий Шапиро-Уилка, критерий Колмогорова-Смирнова и критерий Д’Агостино-Пирсона K²

Фото Лукаса на Pexels

Нормальное распределение, также известное как распределение Гаусса, представляет собой распределение вероятностей, описываемое двумя параметрами : среднее значение и стандартное отклонение. Для нормального распределения 68 % наблюдений находятся в пределах ± одного стандартного отклонения от среднего, 95 % — в пределах ± двух стандартных отклонений и 99,7% находятся в пределах ± трех стандартных отклонений.

Для многих наиболее популярных статистических тестов проверка нормальности необходима для выполнения предположений. В противном случае мы можем сделать неверные выводы и разработать неверные модели.

Но, чтобы завершить распределение данных, статистики не должны полагаться только на графические методы, такие как гистограммы или графики распределения. Также необходимо включить результаты тестов нормальности.

Однако в литературе есть несколько тестов, которые можно использовать для оценки этой нормальности, и становится трудно определить, какой из них является наиболее точным для нашего сценария. Например, в статье [1] упоминается 27 различных тестов на нормальность.

Следовательно, цель этой статьи состоит в том, чтобы описать и сравнить три основных критерия нормальности:

Критерий Шапиро-Уилка
Критерий Колмогорова-Смирнова
Критерий Д’Агостино-Пирсона K²

Эта статья разворачивается следующим образом. . Во-первых, описание каждого из этих тестов (см. раздел 1). Во-вторых, сравнение между тестами и вывод о том, какой метод является оптимальным для использования (см. Раздел 2). Наконец, реализация этих алгоритмов в Python (см. раздел 3).

Гипотеза для тестов K² Шапиро-Уилка и Д’Агостино-Пирсона:

Нулевая гипотеза (H0): данные подчиняются нормальному распределению.
Альтернативная гипотеза (h2): данные не подчиняются нормальному распределению.

Напротив, гипотезы для теста Колмогорова-Смирнова:

Нулевая гипотеза (H0): данные получены из указанного распределения.
Альтернативная гипотеза (h2): по крайней мере одно значение не соответствует указанному распределению.

Если мы считаем, что указанное распределение является нормальным распределением, то мы будем оценивать нормальность.

Если p-значение меньше выбранного альфа-уровня, то нулевая гипотеза отклоняется и имеется свидетельство того, что тестируемые данные не имеют нормального распределения. С другой стороны, если p-значение больше, чем выбранный альфа-уровень, то нулевая гипотеза не может быть отвергнута.

Вот пошаговая методика расчета p-значения для каждого из тестов.

Тест Шапиро-Уилка

Основной подход, используемый в тесте Шапиро-Уилка (SW) для нормальности, заключается в следующем [2].

Во-первых, расположите данные в порядке возрастания так, чтобы x_1 ≤ … ≤ x_n . Во-вторых, рассчитайте сумму квадратов следующим образом:

Затем рассчитайте b следующим образом:

, взяв веса ai из таблицы 1 (на основе значения n ) в таблицах Шапиро-Уилка. Обратите внимание, что если n является нечетным, медианное значение данных не используется при расчете 9.0211 б . Если n четно, пусть m = n /2, а если n нечетно, пусть m = ( n –1)/2.

Наконец, рассчитайте тестовую статистику:

Найдите значение в таблице 2 таблиц Шапиро-Уилка (для заданного значения n ), которое наиболее близко к W , при необходимости интерполируя. Это p-значение для теста.

Этот подход ограничен образцами от 3 до 50 элементов.

Тест Колмогорова–Смирнова

Тест Колмогорова-Смирнова сравнивает ваши данные с заданным распределением и выдает результаты, если они имеют такое же распределение. Хотя тест непараметрический — он не предполагает какого-либо конкретного базового распределения — он обычно используется в качестве теста на нормальность, чтобы увидеть, нормально ли распределены ваши данные [3].

Общие шаги для выполнения теста:

Создайте EDF для ваших выборочных данных (этапы см. в Функция эмпирического распределения ). Эмпирическая функция распределения — это оценка кумулятивной функции распределения, сгенерировавшей точки в выборке.
Укажите родительский дистрибутив (т. е. тот, с которым вы хотите сравнить EDF)
Сопоставьте два дистрибутива вместе.
Измерьте наибольшее расстояние по вертикали между двумя графиками и рассчитайте тестовую статистику, где m и n — размеры выборки.

Рисунок 1 . Пример двухвыборочного теста Колмогорова-Смирнова. Ref : Bскан.

Найдите критическое значение в таблице KS.
Сравните с критическим значением.

Критерий K² Д’Агостино-Пирсона

Критерий K² Д’Агостино-Пирсона вычисляет два статистических параметра, называемых эксцессом и асимметрией, чтобы определить, отклоняется ли распределение данных от нормального распределения: количественная оценка того, насколько распределение сдвинуто влево или вправо, мера асимметрии в распределении.

Эксцесс количественно определяет, какая часть распределения находится в хвосте. Это простой и часто используемый статистический тест на нормальность.

Этот тест сначала вычисляет асимметрию и эксцесс, чтобы количественно определить, насколько далеко распределение от Гаусса с точки зрения асимметрии и формы. Затем он вычисляет, насколько каждое из этих значений отличается от значения, ожидаемого при распределении по Гауссу, и вычисляет одно значение p из суммы этих расхождений [4].

Чтобы ответить на этот вопрос, вот вывод из статьи Asghar Ghasemi et al. (2012) [5], которая имеет более 4000 цитирований:

Согласно имеющейся литературе, при использовании параметрических статистических тестов необходимо учитывать предположение о нормальности. Представляется, что наиболее популярный критерий нормальности, т. е. критерий Колмогорова–Смирнова, больше не следует использовать из-за его малой мощности. Предпочтительно, чтобы нормальность оценивалась как визуально, так и с помощью тестов на нормальность, из которых настоятельно рекомендуется тест Шапиро-Уилка.

Для оценки тестов мы создали четыре выборки, которые различаются размером выборки и распределением:

Первая выборка : 20 данных и нормальное распределение.
Вторая выборка : 200 данных и нормальное распределение.
Третий образец : 20 данных и бета-распределение с ɑ = 1 и β = 5,
Четвертая выборка : 200 данных и бета-распределение с ɑ = 1 и β = 5.

Рисунок 2 . Примеры раздач. Ref : Изображение автора.

В принципе, глядя на графики, тесты на нормальность должны отклонять нулевую гипотезу для четвертой выборки и не должны отклонять ее для второй выборки. С другой стороны, о результатах для первого и третьего образцов трудно судить, просто взглянув на графики.

Тест Шапиро-Уилка

Вот реализация теста Шапиро-Уилка:

 Образец 1: ShapiroResult (статистика = 0,869, pvalue = 0,011) 
 Образец 2: ShapiroResult (статистика = 0,996, pvalue = 0,923) 
 Образец 3: ShapiroResult (статистика = 0,926, pvalue=0,134) 
 Образец 4: ShapiroResult(statistic=0,878, pvalue=1,28e-11)

Результаты показывают, что мы можем отклонить нулевую гипотезу (выборки не подчиняются нормальному распределению) для образцов 1 и 4.

Тест Колмогорова-Смирнова

Вот реализация теста Колмогорова-Смирнова:

 Образец 1: KstestResult (статистика = 0,274, pvalue = 0,081) 
 Образец 2: KstestResult (статистика = 0,091, pvalue = 0,070) 
 Образец 3: KstestResult (статистика = 0,507) , pvalue=2,78e-05) 
 Образец 4: KstestResult(statistic=0,502, pvalue=4,51e-47)

Результаты показывают, что мы можем отклонить нулевую гипотезу (выборки не подчиняются нормальному распределению) для всех выборок .

Поскольку этот тип теста также применим к любому типу распределения, мы можем сравнить выборки между ними.

 Образцы 1 и 2: KstestResult(статистика=0,32, pvalue=0,039) 
 Образцы 3 и 2: KstestResult(статистика=0,44, pvalue=0,001) 
 Образцы 4 и 2: KstestResult(статистика=0,44, pvalue=2,23e- 17)

Критерий K² Д’Агостино-Пирсона

Вот реализация критерия K² Д’Агостино-Пирсона:

 Пример 1: NormaltestResult(statistic=10,13, pvalue=0,006) 
 Sample 2: NormaltestResult( статистика = 0,280, pvalue = 0,869) 
 Образец 3: NormaltestResult (статистика = 2,082, pvalue = 0,353) 
 Образец 4: NormaltestResult(statistic=46.62, pvalue=7.52e-11)

Как и в случае с тестом Шапиро-Уилка, результаты показывают, что мы можем отклонить нулевую гипотезу (выборки не подчиняются нормальному распределению) для образцов 1 и 4.

Проверка нормальности выборки необходима для выполнения предположений многих наиболее популярных статистических тестов.

Тест на определение нормальности: Тест на определение степени вашей нормальности