Что это шкала: Виды шкал и их особенности
Виды шкал и их особенности
Проблема обеспечения высокого качества продукции тесным образом связана с проблемой качества измерений. Между ними явно прослеживается непосредственная связь: там, где качество измерений не соответствует требованиям технологического процесса, невозможно достичь высокого уровня качества продукции. Поэтому качество продукции в значительной степени зависит от успешного решения вопросов, связанных с точностью измерений параметров качества материалов и комплектующих изделий и поддержания заданных технологических режимов. Иными словами, технический контроль качества осуществляется путем замеров параметров технологических процессов, результаты измерений которых необходимы для регулирования процессом.
Следовательно, качество измерений представляет собой совокупность свойств состояния измерений, обеспечивающих результаты измерений с требуемыми точностными характеристиками, получаемые в необходимом виде за определенный отрезок времени.
Основные свойства состояния измерений:
• точность результатов измерений;
• воспроизводимость результатов измерений;
• сходимость результатов измерений;
• быстрота получения результатов;
• единство измерений.
При этом под воспроизводимостью результатов измерений понимается близость результатов измерений одной и той же величины, полученные в разных местах, разными методами, разными средствами, разными операторами, в разное время, однако в одних и тех же условиях измерений (температуре, давлении, влажности и т.д.).
Сходимость результатов измерений — это близость результатов измерений одной и той же величины, проведенных повторно с применением одних и тех же средств, одним и тем же методом в одинаковых условиях и с той же тщательностью.
Любое измерение или количественное оценивание чего-либо осуществляется, используя соответствующие шкалы.
Шкала — это упорядоченный ряд отметок, соответствующий соотношению последовательных значений измеряемых величин.
В метрологии шкала измерений является средством адекватного сопоставления и определения численных значений отдельных свойств и качеств различных объектов. Практически используют пять видов шкал: шкалу наименований, шкалу порядка, шкалу интервалов, шкалу отношений и шкалу абсолютных значений.
Шкала наименований (номинальная шкала). Это самая простая из всех шкал. В ней числа выполняют роль ярлыков и служат для обнаружения и различения изучаемых объектов. Числа, составляющие шкалу наименований, разрешается менять местами. В этой шкале нет отношений типа «больше—меньше», поэтому некоторые полагают, что применение шкалы наименований не стоит считать измерением. При использовании шкалы наименований могут проводится только некоторые математические операции. Например, ее числа нельзя складывать и вычитать, но можно подсчитывать, сколько раз (как часто) встречается то или иное число.
Шкала порядка. Места, занимаемые величинами в шкале порядка, называются рангами, а сама шкала называется ранговой, или неметрической. В такой шкале составляющие ее числа упорядочены по рангам (т.е. занимаемым местам), но интервалы между ними точно измерить нельзя. В отличие от шкалы наименований шкала порядка позволяет не только установить факт равенства или неравенства измеряемых объектов, но и определить характер неравенства в виде суждений: «больше—меньше», «лучше—хуже» и т.п.
С помощью шкал порядка можно измерять качественные, не имеющие строгой количественной меры, показатели. Особенно широко эти шкалы используются в гуманитарных науках: педагогике, психологии, социологии. К рангам шкалы порядка можно применять большее число математических операций, чем к числам шкалы наименований.
Шкала интервалов. Это такая шкала, в которой числа не только упорядочены по рангам, но и разделены определенными интервалами. Особенность, отличающая ее от описываемой дальше шкалы отношений, состоит в том, что нулевая точка выбирается произвольно. Примерами могут быть календарное время (начало летоисчисления в разных календарях устанавливалось по случайным причинам, температура, потенциальная энергия поднятого груза, потенциал электрического поля и др.).
Примерами могут быть календарное время (начало летоисчисления в разных календарях устанавливалось по случайным причинам, температура, потенциальная энергия поднятого груза, потенциал электрического поля и др.).
Результаты измерений по шкале интервалов можно обрабатывать всеми математическими методами, кроме вычисления отношений. Данные шкалы интервалов дают ответ на вопрос «на сколько больше?», но не позволяют утверждать, что одно значение измеренной величины во столько-то раз больше или меньше другого. Например, если температура повысилась с 10 до 20°С, то нельзя сказать, что стало в два раза теплее.
Шкала отношений. Эта шкала отличается от шкалы интервалов только тем, что в ней строго определено положение нулевой точки. Благодаря этому шкала отношений не накладывает никаких ограничений на математический аппарат, используемый для обработки результатов наблюдений.
По шкале отношений измеряют и те величины, которые образуются как разности чисел, отсчитанных по шкале интервалов. Так, календарное время отсчитывается по шкале интервалов, а интервалы времени — по шкале отношений.
При использовании шкалы отношений (и только в этом случае!) измерение какой-либо величины сводится к экспериментальному определению отношения этой величины к другой подобной, принятой за единицу. Измеряя длину объекта, мы узнаем, во сколько раз эта длина больше длины другого тела, принятого за единицу длины (метровой линейки в данном случае) и т.п. Если ограничиться только применением шкал отношений, то можно дать другое (более узкое, частное) определение измерения: измерить какую-либо величину — значит найти опытным путем ее отношение к соответствующей единице измерения.
Шкала абсолютных величин. Во многих случаях напрямую измеряется величина чего-либо. Например, непосредственно подсчитывается число дефектов в изделии, количество единиц произведенной продукции, сколько студентов присутствует на лекции, количество прожитых лет и т.д. и т.п. При таких измерениях на измерительной шкале отмечаются
абсолютные количественные значения измеряемого. Такая шкала абсолютных значений обладает и теми же свойствами, что и шкала отношений, с той лишь разницей, что величины, обозначенные на этой шкале, имеют абсолютные, а не относительные значения.
Такая шкала абсолютных значений обладает и теми же свойствами, что и шкала отношений, с той лишь разницей, что величины, обозначенные на этой шкале, имеют абсолютные, а не относительные значения.
Результаты измерений по шкале абсолютных величин имеют наибольшую достоверность, информативность и чувствительность к неточностям измерений.
Шкалы интервалов, отношений и абсолютных величин называются метрическими, так как при их построении используются некоторые меры, т.е. размеры, принятые в качестве единиц измерений.
Шкалы измерений в метрологии | Виды шкал: номинальные, абсолютные, порядка, отношений, интервалов
Шкала измерений – это совокупность значений, позволяющих количественно или качественно отобразить свойства объекта измерений. Разнообразные проявления (количественные или качественные) любого свойства образуют множества, отображения элементов которых на упорядоченное множество чисел или в более общем случае условных знаков образуют шкалы измерения этих свойств. Шкала измерений количественного свойства является шкалой физической величины. Шкала физической величины — это упорядоченная последовательность значений ФВ, принятая по соглашению на основании результатов точных измерений.
Виды шкал измерений
В практической деятельности необходимо проводить измерения различных величин, характеризующих свойства тел, веществ, явлений и процессов. Некоторые свойства измерительных шкал в метрологии проявляются только качественно, другие — количественно.
Шкала – упорядоченный числовой или символьный ряд значений, отражающий допустимые вариации значений измеряемой величины.
В соответствии с логической структурой проявления свойств различают пять основных видов шкал измерений: шкалы наименований, шкалы порядка, шкалы интервалов, шкалы отношений, абсолютные шкалы.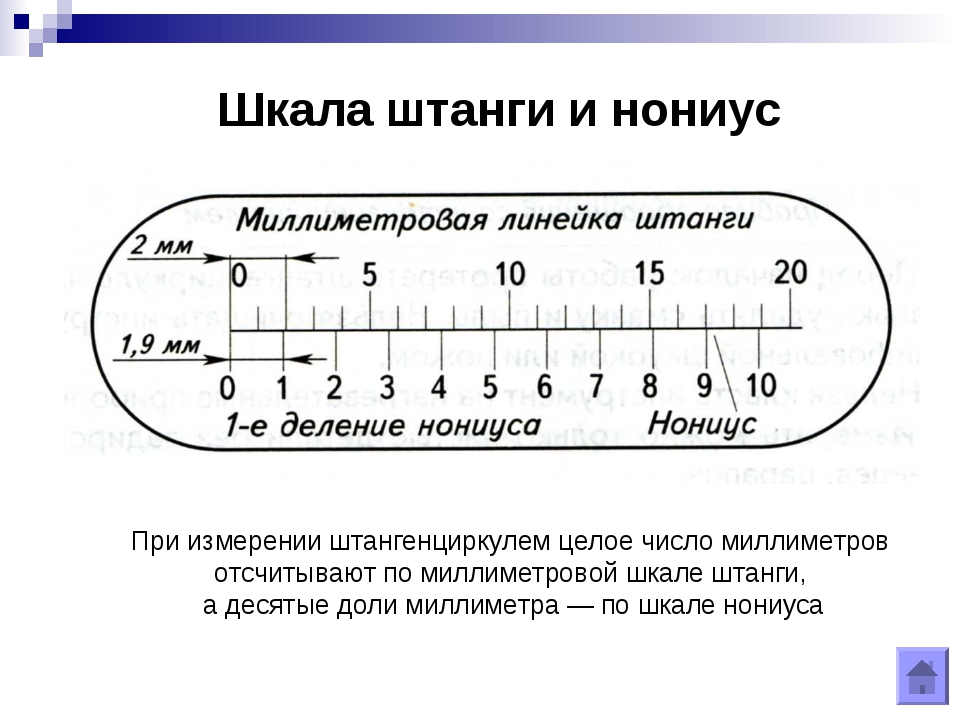
Номинальная шкала (шкала наименований)
Рисунок – Пример номинальной шкалы (атлас цветов)
Такие шкалы измерений в метрологии используются для классификации эмпирических объектов, свойства которых проявляются только в отношении эквивалентности эти свойства нельзя считать физическими величинами, поэтому шкалы такого вида но являются шкалами ФВ. Номинальные шкалы, или, как их еще называют шкалы наименований так же называют шкалами измерений, или шкалами классификаций. Это самый простой тип шкал, основанный на приписывании качественным свойствам объектов чисел, играющих роль имен.
В номинальных шкалах, в которых отнесение отражаемого свойства к тому или иному классу эквивалентности осуществляется с использованием органов чувств человека, наиболее адекватен результат, выбранный большинством экспертов. При этом большое значение имеет правильный выбор классов эквивалентной шкалы — они должны надежно различаться наблюдателями, экспертами, оценивающими данное свойство. Нумерация объектов по шкале наименований осуществляется по принципу: «не приписывай одну и ту же цифру разным объектам». Числа, приписанные объектам, могут быть использованы для определения вероятности или частоты появления данного объекта, но их нельзя использовать для суммирования и других математических операций.
Поскольку данные шкалы характеризуются только отношениями эквивалентности, то в них отсутствует понятия нуля, «больше» или «меньше» и единицы измерения. Примером номинальных шкал являются широко распространенные атласы цветов, предназначенные для идентификации цвета.
Шкала порядка (рангов)
Если свойство данного эмпирического объекта проявляет себя в отношении эквивалентности и порядка по возрастанию или убыванию количественного проявления свойства, то для него может быть построена шкала порядка. Она является монотонно возрастающей или убывающей и позволяет установить отношение больше/меньше между величинами, характеризующими указанное свойство. В шкалах порядка существует или не существует нуль, но принципиально нельзя ввести единицы измерения, так как для них не установлено отношение пропорциональности и соответственно нет возможности судить во сколько раз больше или меньше конкретные проявления свойства.
В случаях, когда уровень познания явления не позволяет точно установить отношения, существующие между величинами данной характеристики, либо применение удобно и достаточно для практики, используют условные (эмпирические) шкалы порядка. Условная шкала — это шкала ФВ, исходные значения которой выражены в условных единицах. Пример шкалы порядка — шкала вязкости Энглера, 12-бальная шкала Бофорта для силы морского ветра.
Рисунок — Пример шкалы порядка (шкала Бофорта)
Широкое распространение получили шкалы измерений порядка с нанесенными на них реперными точками. К таким шкалам, например, относится шкала Мооса для определения твердости минералов, которая содержит 10 опорных (реперных) минералов с различными условными числами твердости: тальк – 1; гипс – 2; кальций – 3; флюорит – 4; апатит – 5; ортоклаз – 6; кварц – 7; топаз – 8; корунд – 9; алмаз – 10. Отнесение минерала к той или иной градации твердости осуществляется на основании эксперимента, который состоит в том, что испытуемый материал царапается опорным. Если после царапанья испытуемого минерала кварцем (7) на нем остается след, а после ортоклаза (6) — не остается, то твердость испытуемого материала составляет более 6, но менее 7. Более точного ответа в этом случае дать невозможно,
В условных шкалах одинаковым интервалам между размерами данной величины не соответствуют одинаковые размерности чисел, отображающих размеры. С помощью этих чисел можно найти вероятности, моды, медианы, квантили, однако их нельзя использовать для суммирования, умножения и других математических операция. Определение значения величин при помощи шкал порядка нельзя считать измерением, так как на этих шкалах не могут быть введены единицы измерения. Операцию по приписыванию числа требуемой величине следует считать оцениванием. Оценивание по шкалам порядка является неоднозначным и весьма условным, о чем свидетельствует рассмотренный пример.
Шкала интервалов (разностей)
Эти шкалы измерений в метрологии являются дальнейшим развитием шкал порядка и применяются для объектов, свойства которых удовлетворяют отношениям эквивалентности, порядка и аддитивности. Шкала интервалов состоит из одинаковых интервалов, имеет единицу измерения и произвольно выбранное начало – нулевую точку. Пример шкалы интервалов — летоисчисление по различным календарям, в которых за начало отсчета принято либо сотворение мира, либо рождество Христово и т.д. Температурные шкалы Цельсия, Фаренгейта и Реомюра также являются шкалами интервалов.
Шкала интервалов состоит из одинаковых интервалов, имеет единицу измерения и произвольно выбранное начало – нулевую точку. Пример шкалы интервалов — летоисчисление по различным календарям, в которых за начало отсчета принято либо сотворение мира, либо рождество Христово и т.д. Температурные шкалы Цельсия, Фаренгейта и Реомюра также являются шкалами интервалов.
Рисунок – Пример шкалы интервалов (Температурные шкалы Цельсия и Фаренгейта)
На шкале интервалов определены действия сложения и вычитания интервалов. Действительно, по шкале времени интервалы можно суммировать или вычитать и сравнивать, во сколько раз один интервал больше другого, но складывать даты каких-либо событий просто бессмысленно.
Шкала интервалов величины Q описывается уравнением Q = Qо + q[Q], где q — числовое значение величины; Qо — начало отсчета шкалы; [Q] — единица рассматриваемой величины. Такая шкала полностью определяется заданием начала отсчета Qо шкалы и единицы данной величины [Q].
Задать шкалу практически можно двумя путями. При первом из них выбираются два значения Qо и Q1, величины, которые относительно просто реализованы физически. Эти значения называются опорными точками, или основными реперами, а интервал (Q1 ~ Qо) — основным интервалом. Точка Qо принимается за начало отсчета, а величина (Q1 -Qо)/n=[Qо] за единицу Q. При этом n выбирается таким, чтобы [Q] было целой величиной.
Рисунок – Пример шкалы отношений
При втором пути задания шкалы единица воспроизводится непосредственно как интервал, его некоторая доля или некоторое число интервалов размеров данной величины, а начало отсчета выбирают каждый раз по-разному в зависимости от конкретных условий изучаемого явления. Пример такого подхода — шкала времени, в которой 1с = 9192631770 периодов излучения, соответствующих переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133. За начало отсчета принимается начало изучаемого явления.
За начало отсчета принимается начало изучаемого явления.
Шкала отношений
Шкала отношений описывает свойства эмпирических объектов, которые удовлетворяют отношениям эквивалентности, порядка и аддитивности (шкалы второго рода — аддитивные), а в ряде случаев и пропорциональности (шкалы первого рода — пропорциональные). Пример шкалы отношений — шкала массы (второго рода), термодинамической температуры (первого рода).
В шкалах отношений существует однозначный естественный критерий нулевого количественного проявления свойства и единица измерений, установленная по соглашению. С формальной точки зрения этот вид шкал измерений является шкалой интервалов с естественным началом отсчета. К значениям, полученным по этой шкале, применимы все арифметические действия, что имеет важное значение при измерений физических величин.
Рисунок – Пример абсолютной шкалы (шкала температур Кельвина)
Шкалы отношений — самые совершенные. Они описываются уравнением Q = q[Q], где Q — ФВ, для которой строится шкала, [Q] — ее единица измерения, q — числовое значение ФВ. Переход от одной шкалы отношений к другой происходит в соответствии с уравнением q2 = q1[Q1]/[Q2].
Абсолютные шкалы
Абсолютные шкалы — это шкалы, обладающие всеми признаками шкал отношений, но дополнительно имеющие естественное однозначное определение единицы измерения и не зависящие от принятой системы единиц измерения. Примером абсолютной шкалы могут стать шкалы с относительным величинам: коэффициенту усиления, ослабления и др. Для образования многих производных единиц в системе СИ используются безразмерные и счетные единицы абсолютных шкал.
Отметим, что шкалы наименований и порядка называют неметрическими (концептуальными), а шкалы интервалов и отношений — метрическими (материальными). Метрические и абсолютные шкалы относятся к разряду линейных. Практическая реализация шкал измерений в метрологии осуществляется путем стандартизации как самих шкал и единиц измерений, так и, в необходимых случаях, способов и условий их однозначного воспроизведения.
Изготовление измерительной шкалы своими руками
Видео о том, как самостоятельно сделать шкалу стрелочного прибора на примере изготовления шкалы амперметра.
Похожие материалы
Шкала — это… Что такое Шкала?
Шкала — это знаковая система, для которой задано гомоморфное отображение, ставящее в соответствие реальным объектам тот или иной элемент шкалы. Формально шкалой называют кортеж, <X, φ, Y>, где X — реальный объект, φ — отображение, Y — знаковая система[1].
Различные типы измерительных шкал широко используются в физике, технике, экономике, психометрии, социологии и других приложениях[2][3]
Типы шкал
Шкалы измерений принято классифицировать по типам измеряемых данных, которые определяют допустимые для данной шкалы математические преобразования, а также типы отношений, отображаемых соответствующей шкалой [1], [4]. Современная классификация шкал была предложена в 1946 году Стэнли Смитом Стивенсом.
- Шкала наименований (номинальная, классификационная)
- Используется для измерения значений качественных признаков. Значением такого признака является наименование класса эквивалентности, к которому принадлежит рассматриваемый объект. Примерами значений качественных признаков являются названия государств, цвета, марки автомобилей и т.п. Такие признаки удовлетворяют аксиомам тождества:
- Либо А = В, либо А ≠ В;
- Если А = В, то В = А;
- Если А = В и В = С, то А = С.
- При большом числе классов используют иерархические шкалы наименований. Наиболее известными примерами таких шкал являются[5] шкалы, используемые для классификации животных и растений.
- С величинами, измеряемыми в шкале наименований, можно выполнять только одну операцию — проверку их совпадения или несовпадения.
 По результатам такой проверки можно дополнительно вычислять частоты заполнения (вероятности) для различных классов, которые могут использоваться для применения различных методов статистического анализа[5] — критерия согласия Хи-квадрат, критерия Крамера для проверки гипотезы о связи качественных признаков и др.
По результатам такой проверки можно дополнительно вычислять частоты заполнения (вероятности) для различных классов, которые могут использоваться для применения различных методов статистического анализа[5] — критерия согласия Хи-квадрат, критерия Крамера для проверки гипотезы о связи качественных признаков и др. - Порядковая шкала (или ранговая)
- Строится на отношении тождества и порядка. Субъекты в данной шкале ранжированы. Но не все объекты можно подчинить отношению порядка. Например, нельзя сказать, что больше круг или треугольник, но можно выделить в этих объектах общее свойство-площадь, и таким образом становится легче установить порядковые отношения. Для данной шкалы допустимо монотонное преобразование. Такая шкала груба, потому что не учитывает разность между субъектами шкалы. Пример такой шкалы: балльные оценки успеваемости в УАБД НБУ г.Сумы (неудовлетворительно, удовлетворительно, хорошо, отлично), шкала Мооса.
- Интервальная шкала (она же Шкала разностей)
- Здесь происходит сравнение с эталоном. Построение такой шкалы позволяет большую часть свойств существующих числовых систем приписывать числам, полученным на основе субъективных оценок. Например, построение шкалы интервалов для реакций. Для данной шкалы допустимым является линейное преобразование. Это позволяет приводить результаты тестирования к общим шкалам и осуществлять, таким образом сравнение показателей. Пример: шкала Цельсия.
- Начало отсчёта произвольно, единица измерения задана. Допустимые преобразования — сдвиги. Пример: измерение времени.
- Абсолютная шкала (она же Шкала отношений)
- это интервальная шкала, в которой присутствует дополнительное свойство — естественное и однозначное присутствие нулевой точки. Пример: число людей в аудитории. В шкале отношений действует отношение «во столько-то раз больше». Это единственная из четырёх шкал имеющая абсолютный ноль. Нулевая точка характеризует отсутствие измеряемого качества. Данная шкала допускает преобразование подобия (умножение на константу).
 Определение нулевой точки — сложная задача для психологических исследований, накладывающая ограничение на использование данной шкалы. С помощью таких шкал могут быть измерены масса, длина, сила, стоимость (цена). Пример: шкала Кельвина (температур, отсчитанных от абсолютного нуля, с выбранной по соглашению специалистов единицей измерения — Кельвин).
Определение нулевой точки — сложная задача для психологических исследований, накладывающая ограничение на использование данной шкалы. С помощью таких шкал могут быть измерены масса, длина, сила, стоимость (цена). Пример: шкала Кельвина (температур, отсчитанных от абсолютного нуля, с выбранной по соглашению специалистов единицей измерения — Кельвин).
Из рассмотренных шкал первые две являются неметрическими, а остальные — метрическими.
С вопросом о типе шкалы непосредственно связана проблема адекватности методов математической обработки результатов измерения. В общем случае адекватными являются те статистики, которые инвариантны относительно допустимых преобразований используемой шкалы измерений.
Использование в психометрии
Используя различные шкалы, можно производить различные психологические измерения. Самые первые методы психологических измерений были разработаны в психофизике. Основной задачей психофизиков являлось то, каким образом определить, как соотносятся физические параметры стимуляции и соответствующие им субъективные оценки ощущений. Зная эту связь, можно понять, какое ощущение соответствует тому или иному признаку. Психофизическая функция устанавливает связь между числовым значением шкалы физического измерения стимула и числовым значением психологической или субъективной реакцией на этот стимул.
Некоторые распространённые шкалы
См. также
Примечания
(PDF) Тест — это шкала. Какая? Test is a scale. Which?
В качестве функции успеха обычно выбирается логистическая функ-
ция. Однако выбор логистической функции обусловлен лишь ее близостью
к интегральной нормальной функции распределения [8, с. 262], простотой
ее алгебраического выражения и вытекающей из этого простотой и эконо-
мичностью математических расчетов. В настоящее время, при значительно
возросших вычислительных мощностях, встает вопрос об отказе от моде-
лей логистического семейства (Раша, Бирнбаума) и переходе к параллель-
ным (по количеству параметров) моделям с функцией успеха на базе нор-
мальной огивы (что, впрочем, и предполагалось изначально в работах
классиков тестирования [11, с. 90]). Открытым остается вопрос, соответ-
90]). Открытым остается вопрос, соответ-
ствует ли нормальное распределение природе измеряемого объекта. Соци-
альный характер измеряемого свойства предполагает отрицательный ответ,
и альтернативной должно служить распределение с более длинным «хво-
стом», в качестве которого нами ранее предлагалось распределение Коши,
что предполагает функцию успеха на основе тангенсоиды.
Лишь определившись с видом распределения измеряемой перемен-
ной (в классической тестовой теории) или с видом функции успеха (в со-
временных теориях тестирования), можно вновь вернуться к интересую-
щему нас вопросу о типе измерительной шкалы.
Принято считать, что результаты педагогических измерений в рам-
ках классической тестовой теории определяются на шкале порядка (ранго-
вой). Это предположение справедливо «в среднем». При тщательной
настройке теста и его стандартизации удается выразить результаты на бо-
лее мощной интервальной шкале. При низком качестве теста тест оказыва-
ется не в состоянии правильно ранжировать испытуемых, и поскольку со-
гласно классификации Стивенса существует лишь один тип шкалы менее
мощной, чем ранговая – шкала наименований (номинальная шкала), тести-
рование сведется к констатации факта, что i-му испытуемому свойственен
уровень подготовленности «Аi», где Аi – не число, а «имя», приписанное
испытуемому. Нас, безусловно, интересует возможность выражения ре-
зультата на интервальной шкале, что возможно лишь в случае тщательного
отбора заданий по валидности и степени трудности. Как говорилось выше,
на нормативной (репрезентативной) выборке испытуемых распределение
тестовых результатов должно соответствовать выбранному каноническому
распределению.
После пилотного тестирования (предтестирования) необходимо про-
верить соответствие эмпирического распределения теоретическому и вне-
сти необходимые коррективы в тест, удаляя либо добавляя задания. Трудо-
Трудо-
емкость процедуры побуждает отказаться от классической тестовой теории
в пользу современных теорий тестирования, основанных на функции успе-
ха.
Из современных моделей самой простой является однопараметриче-
ская модель Раша [8, с. 262], положенная в настоящее время в основу об-
Понятие шкалы измерения, виды шкал в социологическом исследовании
Шкала измерения
Определение 1
Шкала — это особый способ измерения социального объекта.
Измерение в социологии понимается в двух аспектах:
- теоретически, в рамках дискуссии о применимости математических методов в социологических исследованиях, их возможностях, границах, характере качественных и количественных методов;
- эмпирически, как построение шкал.
При изучении социальной реальности социолога, как правило, интересуют отношения, в которые входит объект исследования (например, как мы относимся к нашей профессии, к нашему учебному заведению, к тому или иному виду деятельности). Чтобы как-то исправить, «поймать» эти отношения, социолог соотносит их с любой числовой системой. Числовая система представляет собой шкалу
Виды шкал в социологическом исследовании
Вы можете классифицировать шкалы по объекту измерения. Это либо оценка внешних объектов, либо характеристики внутренних состояний предметных мотивов, установок, знаний, навыков и т. Д. Поэтому шкалы делятся на шкалы оценок и шкалы установок.
Шкалы оценки были первыми, которые были применены в социологической практике. Самым простым типом оценочной шкалы является школьная система баллов. В начале XX века известный статистик К. Пирсон использовал эту шкалу для изучения способностей, после чего шкалы оценки стали широко распространенными. Шкала оценки включает три компонента:
- тот, кто оценивает;
- что оценивается;
- относительно того, что оценивается.
Оценочные шкалы представлены в двух вариантах: графическая (графическая) и описательная (словесная характеристика) шкалы. Впервые шкала оценки использовалась Богардусом для социологических исследований в 1925 году. Затем были разработаны методы построения шкал установок. Этому способствовали Турстон, Ликерт, Гутман.
Впервые шкала оценки использовалась Богардусом для социологических исследований в 1925 году. Затем были разработаны методы построения шкал установок. Этому способствовали Турстон, Ликерт, Гутман.
Еще одним критерием классификации шкал является уровень измерения. Основой этого типа измерений является использование все более разнообразного и сложного математического аппарата в статистическом анализе полученных данных. Поэтому в противном случае этот критерий классификации можно определить как «характер использования математического аппарата». Результатом сложности анализа данных является получение данных с более высокой степенью точности, достоверности, возможность фиксации более «тонкой» информации, соответствующей целям исследования.
Поскольку числовые системы различаются по разнообразию операций с числами (когда в одних возможны только самые простые арифметические операции, в других — самые разные по степени сложности), то речь идет о множестве шкал, различающихся по уровню использования. математического аппарата.
Типы шкал, классифицированные по этому критерию, имеют две подгруппы — номинальные шкалы и метрические.
Номинальные шкалы, в свою очередь, делятся на номинальные неупорядоченные, номинальные, частично упорядоченные и порядковые (одной из разновидностей которых является шкала рангов).
Метрические шкалы включают интервальные и абсолютные шкалы.
Номинальная неупорядоченная шкала (неупорядоченная шкала именования) представляет собой «самый низкий» уровень измерения. Это дает минимальный объем информации. Элементы шкалы — это классификация свойств объекта, их простое имя, поэтому шкалу иногда называют шкалой имен. Соотношение равенства установлено между всеми этими свойствами.
Порядковая шкала — это такая шкала измерений, которая позволяет судить о том, какие особенности объекта характеризуются большим, а какие — меньшим количеством измеряемого свойства. Между точками шкалы устанавливаются отношения «более — менее». С помощью этих шкал вы можете измерить интенсивность оценок любых свойств, суждений.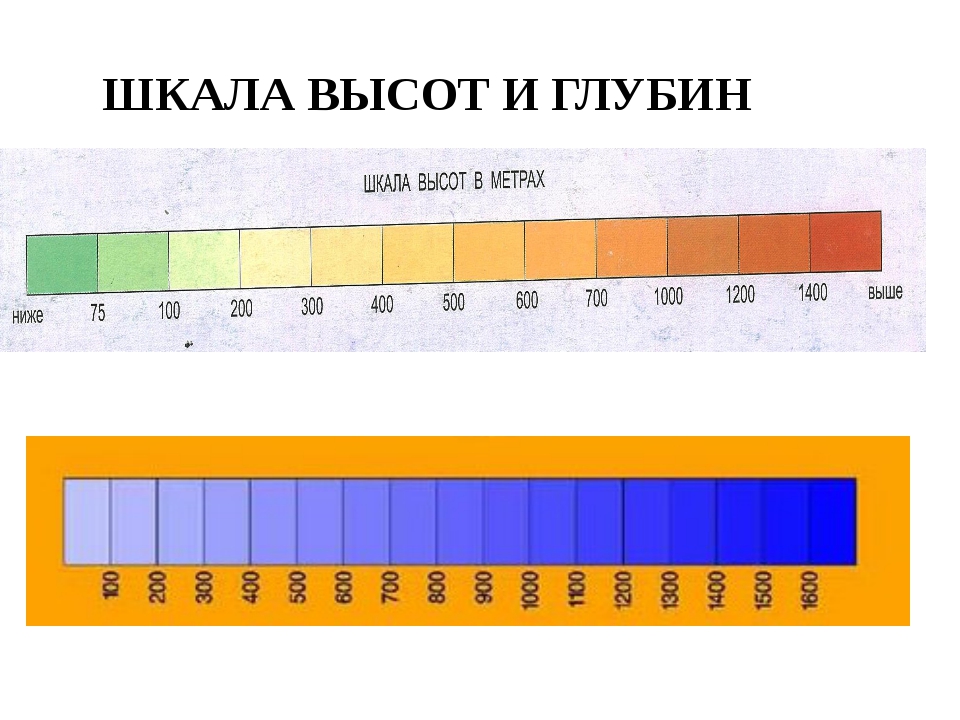
Видом шкал этого типа являются раногвые шкалы. Ранги могут быть установлены самим объектом. По просьбе исследователя он организует суждения, предложенные ему, в порядке от наиболее важных для него до наименее важных. Таким образом, согласно типу шкалы рангов, можно построить процедуру измерения потребности в образовании, знаниях определенного типа. Например, «какие знания важнее всего для вас?» (Расставьте ответы в порядке убывания важности). Сложность этой процедуры заключается в том, что зачастую необходимо выяснить отношение ответчика к большому количеству должностей, например, существует более пятнадцати. Это снижает возможности (стабильность, надежность) весов и частоту их использования.
Частично упорядоченная шкала — это переходный тип шкалы, в котором некоторые элементы упорядочены, а некоторые нет.
В некоторых случаях это связано с тем, что признаки классифицируются более чем по одному критерию. И чаще всего неупорядоченные фрагменты шкал возникают, когда для повышения надежности шкал используются пункты «Мне трудно ответить», «Я не знаю», «Трудно сказать», которые «выпадают» из общего порядка. Важность этих моментов трудно переоценить, они позволяют респондентам, «оставляя» в этом вопросе, не фальсифицировать свои собственные неотраженные мнения, суждения, оценки по тем вопросам, в которых у них недостаточно знаний или нет четкой стабильной позиции.
Таким образом, измерение в номинальной неупорядоченной шкале представляется в виде классификации объектов в упорядоченном порядке с фиксированными метрическими интервалами (либо со свободной, либо экспериментально установленной контрольной точкой). Измерение в социологии является одной из важных проблем, от которой и зависит результат социологического исследования. А его практическое значение заключается в способности использования математических методов для измерения каких-то определенных социальных характеристик. Начальные сведения в социологии, полученные в процессе сбора эмпирической информации, как правило, являются качественными. А это, в свою очередь, сильно ограничивает возможности использования математических методов
А это, в свою очередь, сильно ограничивает возможности использования математических методов
При определении типа шкалы, необходимо измерить ее с учетом характера объекта, цели исследования и возможностей количественного анализа. Абсолютно любой статистический анализ всегда должен основываться на надежном стандарте измерения: теоретически обоснованном и эмпирически доказанном. Эффективное измерение требует баланса между качественным и количественным видом анализа.
ГБУЗ «СОДКБ им. Н.Н.Ивановой» Платные услуги
Описание
Шкала CAT/CLAMS и KID — это русская версия Кентской шкалы оценки развития младенцев (Kent Infant Development Scale; KID Scale). KID Scale разработана группой сотрудников Кентского университета (США) под руководством профессора Ж. Рейтер. К настоящему времени KID Scale является распространенной методикой оценки развития детей в ряде стран Западной и Восточной Европы (Испания, Нидерланды, Венгрия, Чехия и др.).
Шкала предназначена для оценки уровня развития детей в возрасте от 2 до 16 месяцев, а также тех детей, чей биологический возраст больше указанного, но возраст развития не превышает 16месяцев.
Как выглядит шкала CAT/CLAMS и KID? И как их оценить?
Шкалы KID представляют собой вопросник, состоящий из 256 пунктов и составленный по результатам анализа разнообразных типичных форм поведения ребенкам первых лет жизни. На первый взгляд, кажется все просто, вопросники заполняют родители ребенка или любой человек, который постоянно с ним общается. Никаких специальных знаний для заполнения бланков анкеты не требуется — достаточно внимательно прочесть и правильно понять инструкцию и вопросы шкалы.
Зачем нужна оценка по шкале CAT/CLAMS и KID?
Важно своевременно выявить текущее состояние уровней развития ребенка по 5-ти основных областям развития ребенка (когнитивная, двигательная, речевая, социальная и самообслуживание)
В случае отставания — разработка программ раннего вмешательства с учетом выявленного возраста развития ребенка.
И конечно, важна оценка в динамики развития ребенка, т.к. именно она покажет эффективность терапии/реабилитации маленького пациента. И здесь очень важна совместная работа психолога и врачей реабилитологов.
Так выглядит шкала после её обработки.
Для детей с 14 месяцев до 3,5 лет существует специальная шкала — ШКАЛА RCDI
Шкала RCDI — это адаптированный к условиям России вариант Шкалы оценки развития ребенка (Child Development Inventory; CDI), разработанной доктором Г. Айртоном (Миннеаполис, США).
Шкала представляет собой вопросник, состоящий из 216 пунктов.
Каждый пункт шкалы отнесен к одной из 6 областей (5 пунктов отнесены одновременно к 2 областям): социальная, самообслуживание, крупные движения, тонкие движения, развитие речи, понимание языка.
Результат применения
Результатом применения шкалы RCDI является оценка возраста развития ребенка и степени его отставания от типично развивающихся сверстников в каждой из областей.
Затем следует кропотливая комплексная работа по восстановлению ребенка, которая ложится на плечи врачей различных специальностей, которые подбирают наиболее подходящие методы реабилитации ребенку, а их арсенал весьма и весьма широк. И конечно, крайне важно желание и стремление самих родителей в процессе лечения и социальной адаптации малыша.
Получить более подробную информацию и записаться на прием можно по следующим телефонам:
- (846) 207-30-78 — Отделение медицинской реабилитации
что это такое и как была разработана
Шкала магнитуды землетрясений Рихтера: появление, принцип вычислений и какими приборами измеряется
Землетрясение – это стихийное бедствие, от которого страдают жители сейсмоактивных территорий Земли. Землетрясение приходит почти всегда внезапно и молниеносно разрушает целые города, проводя черту между «до» и «после».
Но даже в таком внезапном и разрушительном явлении ученые давно нашли варианты по наблюдению, вычислению и подсчетам силы подземных толчков. Шкала Рихтера, о которой мы будем сегодня говорить, как раз и является единицей измерения силы землетрясения и широко используется в сейсмологии по наши дни.
Шкала Рихтера, о которой мы будем сегодня говорить, как раз и является единицей измерения силы землетрясения и широко используется в сейсмологии по наши дни.
Шкала Рихтера является международной единицей измерения, которая определяет и классифицирует величины: силу и скорость сотрясений земной коры при начале сейсмической активности.
Шкала основана на измерении энергии, выделяемой перемещением коры в эпицентре. Сила землетрясения отсчитывается от энергии, то есть магнитуды землетрясения. Магнитуда землетрясения – величина, характеризующая энергию, выделившуюся при землетрясении в виде сейсмических волн.
Стоит отметить, что магнитуда (шкала Рихтера) – это не то же самое, что интенсивность землетрясения. Последнюю высчитывают по шкалам интенсивности волн в земной поверхности.
Интенсивность землетрясения – мера величины сотрясения земной поверхности при землетрясении на охваченной им территории.
История появления шкалы Рихтера
Эта шкала была разработана в 1935 году Чарльзом Фрэнсисом Рихтером и Бено Гутенбергом в Калифорнийском технологическом институте. Первоначально она была названа как шкала ML (Magnitude Local). Ее так обозначают до сих пор: «ML» или «ML», но называют все именно «шкалой Рихтера».
При этом шкала Рихтера, разработанная Чарльзом Ф. Рихтером, не является ни инструментом, ни измерительным (линейкой со шкалой) или, по сути, каким-либо другим прибором. «Шкала» в данном случае – это математическая формула (десятичный логарифм), которая определяет величину и силу землетрясения.
С помощью шкалы Рихтера невозможно измерить величину землетрясений магнитудой более 8. Для измерения силы очень мощных землетрясений используются другие методы.
Шкалы интенсивности землетрясений в разных странах разные, к примеру:
фото: flickr. com
com
В России это 12-балльная шкала Медведева-Шпонхойера-Карника;
В Европе применяется также 12-балльная Европейская макросейсмическая шкала;
В США – 12-балльная модифицированная шкала Меркалли;
В Японии, известной своими землетрясениями, – 7-балльная шкала Японского метеорологического агентства.
Шкала Рихтера была разработана в 1935 году американским сейсмологом Чарльзом Рихтером и его коллегой Бено Гутенбергом как способ количественной оценки величины или силы землетрясений. Рихтер, изучавший землетрясения в Калифорнии в то время, нуждался в простом способе точно выразить то, что качественно было очевидно и тогда: что одни землетрясения малы (поверхностны), а другие велики (глубоки). Но хоть это и было очевидно, доказательств тому не было.
Современные сейсмологи в первую очередь смотрят в корень проблемы – в разломы. Сегодня землетрясения и движение разломов неразрывно связаны в сознании сейсмологов – настолько, что, услышав о произошедшем землетрясении, они сразу же спрашивают о разломе, который его вызвал.
Например, землетрясение магнитудой 6,9 в 1994 году в Нортридже, которое привело к серьезным разрушениям в Лос-Анджелесе, было вызвано движением двух-четырех-метрового пласта в разломе длиной около 12 и шириной 15 километров.
Но когда Чарльз Рихтер взялся за вопрос, его внимание, напротив, было сосредоточено на самой вибрации земли, которую он мог легко отслеживать с помощью сейсмометров в Калифорнийском технологическом институте (Caltech). Для Рихтера землетрясение большой магнитуды было землетрясением лишь с сильной вибрацией Земли. Таким образом, для шкалы Рихтера нет прямой связи ни с одним из свойств первичного разлома, что вносило некую путаницу для понимания обывателями (то есть нами с вами, не связанным с сейсмологией).
Смотрите также
Шкала Рихтера была смоделирована на основе шкалы звездных величин, используемой астрономами, которая количественно определяет объем света, испускаемого звездами (их светимость). Светимость звезды основана на телескопических наблюдениях ее яркости, которые корректируются для увеличения телескопа и расстояния звезды от Земли. Но поскольку светимость колеблется во многих десятках раз (например, Бетельгейзе в 50 000 раз ярче Альфы Центавры), астрономы вычисляют логарифм светимости, чтобы получить звездную величину: легко запоминаемое однозначное число.
Светимость звезды основана на телескопических наблюдениях ее яркости, которые корректируются для увеличения телескопа и расстояния звезды от Земли. Но поскольку светимость колеблется во многих десятках раз (например, Бетельгейзе в 50 000 раз ярче Альфы Центавры), астрономы вычисляют логарифм светимости, чтобы получить звездную величину: легко запоминаемое однозначное число.
Рихтер заменил измерения логарифма светимости на искомые – количество колебаний грунта, измеренные сейсмографом. Заметим, что в обоих случаях понятие силы довольно абстрактно: звездная величина – это не мера физического размера звезды (как можно было бы определить по ее диаметру), а скорее количество света, которое испускает звезда.
Сейсмическая величина – это не мера физического размера разлома землетрясения (как можно было бы количественно определить по его площади или его скольжению), а скорее величина вибрации, которую она испускает.
фото: flickr.com
Аналог шкалы Рихтера определяется количеством энергии, выделяющейся от взрыва, и следующей после него сейсмической реакции волн земной коры.
Например, при землетрясении силой 2 балла выделяется количество энергии, равное 56 килограммам взрывчатого вещества. Конечно, поскольку эта энергия высвобождается на очень большой территории, мы даже ничего не чувствуем. Но когда площадь ограничена – мини-землетрясение будет ощутимым.
Также шкала Рихтера дает информацию не только о величине землетрясения, но и об энергии, выделяющейся при нем.
Разрушительная сила землетрясения пропорциональна 2/3 силы амплитуды колебания. Поэтому, когда интенсивность землетрясения увеличивается на одну единицу по шкале Рихтера, разрушительная сила землетрясения увеличивается в 10 (3/2) = 31,6 раза.
К примеру, магнитуда 3 – это крошечное землетрясение. Магнитуда в 6 баллов – это та величина, которая может нанести существенный ущерб. Магнитуда 9 может вызвать даже цунами, подобно тому, что наблюдалось в декабре 2004 года в Индийском океане .
Магнитуда 9 может вызвать даже цунами, подобно тому, что наблюдалось в декабре 2004 года в Индийском океане .
фото: flickr.com
В первоначальной формулировке Рихтера землетрясение на расстоянии 100 километров, которое вызвало сигнал амплитудой в один миллиметр на бумажном регистраторе сейсмометра Калтеха, было произвольно определено как магнитуда 3 (увеличение сейсмометра Рихтера составило около 2800, поэтому один миллиметр на бумажной записи соответствует примерно 0,36 микрона фактического движения Земли). Землетрясение на том же расстоянии, которое произвело 10-миллиметровую амплитудную запись, было обозначено магнитудой 4, 100-миллиметровая амплитуда – магнитудой 5 и так далее. В дальнейшем Рихтер разработал корректирующие таблицы, которые позволяли вычислять величины независимо от фактического расстояния землетрясения от сейсмометра.
фото: flickr.com
Также магнитуда может быть легко определена из измерений, сделанных сейсмометром, который не должен быть расположен особенно близко к разлому. Действительно, современные сейсмометры могут регистрировать землетрясения магнитудой 5 и выше, происходящие в любой точке мира. Недостатком шкалы Рихтера является то, что величина – это единственное число, которое не может полностью охарактеризовать сложное явление, такое как землетрясение. Землетрясения с одинаковой магнитудой могут различаться многими фундаментальными способами, в том числе направлениями колебаний и их относительной амплитудой в разные периоды во время толчков. Эти различия могут привести к землетрясениям одинаковой величины, имеющим существенно разный уровень разрушительности.
Фактически с помощью современных чувствительных сейсмографов можно идентифицировать землетрясения с отрицательным значением по шкале Рихтера.
Разрушительная сила землетрясения пропорциональна 2/3 силы амплитуды колебания. Поэтому, когда интенсивность землетрясения увеличивается на одну единицу по шкале Рихтера, разрушительная сила землетрясения увеличивается в 10 (3/2) = 31,6 раза.
Развитие теории
фото: Pinterest
И, наконец, начиная с середины 1960-х годов, сейсмологи добились довольно полного понимания того, как скользящий разлом порождает колебания грунта. Важной величиной, характеризующей прочность разлома, является сейсмический момент – алгебраическое произведение площади разлома, скольжения разлома и жесткости окружающей породы.
Как говорят сейсмологи, землетрясение с большой магнитудой соответствует разлому с большим моментом, причем увеличение на единицу величины соответствует увеличению момента примерно в 30 раз. Но эта связь неточна, есть много случаев, когда небольшие сдвиги вызывают неожиданно большое землетрясение или наоборот.
Калькулятор музыкальной шкалы
Калькулятор музыкальной шкалы поможет вам найти ноты шкалы — будь то ноты в крупной шкале, ноты в малой шкале или что-то более экзотическое, например, испанская восьмитональная шкала. это в нашем длинном списке музыкальных гамм.
Калькулятор также выдает образец полутона и числовую формулу определенного масштаба. В то время как ноты шкалы сообщают вам, какие звуки вы можете использовать в данной шкале, полутоновый рисунок показывает, какие интервалы в ней встречаются, а числовая формула сообщает вам, как построить эту шкалу.
Если вас интересует музыка, вот еще несколько калькуляторов, которые могут вам пригодиться:
Как пользоваться калькулятором музыкальной шкалы?
Калькулятор музыкальной гаммы позволяет находить ноты в гамме, числовой формуле и полутоновом шаблоне. Все три результата отображаются по умолчанию, но в расширенном режиме
Выберите корневую ноту — первую ноту гаммы, на которой строится гамма.Например, если вы ищете ноты до мажор, вы, очевидно, должны выбрать C в качестве основной ноты.
 Пропустите этот шаг, если вас не интересуют ноты музыкальной гаммы и вы просто хотите получить полутоновый узор.
Пропустите этот шаг, если вас не интересуют ноты музыкальной гаммы и вы просто хотите получить полутоновый узор.Выберите категорию , в которую, по вашему мнению, попадает ваша шкала. Если вы не уверены, посмотрите список музыкальных гамм внизу статьи (некоторые категории могут быть произвольными).
Выберите название шкалы .
Проверьте результат внизу — ноты шкалы, числовую формулу и полутоновый узор.
Прочтите, чтобы узнать, что означают числа в формулах и как построить весы.
Крупные банкноты
Давайте посмотрим на паттерн полутонов мажорной гаммы :
2, 2, 1, 2, 2, 2, 1
Цифры представляют количество полутонов (полутонов) между последовательными нотами (называемыми градусами шкалы). 1 означает один полутон, 2 означает два полутона (целый тон), 3 означает три полутона и 4 означает два полных тона.
Образец мажорной гаммы выше говорит: есть 2 полутона между первой и второй нотой гаммы, 2 полутона между второй и третьей нотой, 1 полутон между третьей и четвертой и так далее.
Пример :
Давайте построим мажорную шкалу, используя приведенный выше образец:
- Первая нота — это основная нота — A.
- Вторая нота должна быть на 2 полутона (целый шаг) выше, чем A, поэтому это B.
- Третья нота — от B идем еще на один шаг вверх. Между B и C есть полутон, поэтому нам нужно поднять C на полутон. Вы получаете C♯.
- Четвертая нота — 1 полутон выше C♯ — это D.
- Пятая нота — 2 полутона выше D — E.
- Шестая нота — 2 полутона от E — это F♯.
- Седьмая нота — 2 полутона от F♯ — это G♯.
- Восьмая нота в мажорной гамме — это снова первая нота — A.

Таким образом, мы нашли ноты в крупном масштабе A:
A, B, C♯, D, E, F♯, G♯, A
Как найти ноты в гамме?
Используя числовую формулу, вы можете построить шкалу на основе основной шкалы. Цифры в числовой формуле обозначают градусы (ноты) шкалы . 1 — основная нота, 2 — вторая нота и так далее.
Случайности рядом с числами говорят вам, следует ли вам поднять (♯) или опустить (♭) банкноту большой шкалы, чтобы получить желаемую шкалу.Если у вас есть два диеза / бемоля, вы поднимаете / опускаете ноту на полтона дважды.
Пример :
Построим масштаб до минор:
Начальной точкой является до мажор , который вы можете построить, используя полутоновый паттерн:
1: C 2: D 3: E 4: F 5: G 6: A 7: B 8: C(Первая нота — C, вторая — D, и так далее …)
Затем мы проверяем формулу на натуральный минор :
1, 2, 3, 4, 5, 6, 7, 8Теперь мы применяем формулу для минорной гаммы к мажорным нотам :
- Первая нота не меняется, это просто 1, поэтому C.
- Вторая нота также остается D.
- Третья нота — рядом с цифрой 3 стоит плоский знак, поэтому мы должны понизить третью ноту шкалы до мажор — E — на полутон. Получаем E ♭.
- Четвертая нота остается прежней — F.
- Пятая нота остается прежней — G.
- Шестая нота — ♭ 6 означает, что мы опускаем ля на полутон. Получаем A ♭.
- Седьмая нота — опускаем B и получаем B ♭.
- Восьмая нота остается C.
Вот результат — ноты до минор:
C, D, E ♭, F, G, A ♭, B ♭, C
Список гамм
Вот алфавитный список музыкальных гамм, включенных в калькулятор музыкальных гамм, и категории, которым они назначены:
| Id | Название шкалы | Категория | ||||
|---|---|---|---|---|---|---|
| 1 | Акустический | Этнический | ||||
| 2 | Эолийский | Режимы | ||||
| 3 | Алжирский | 902 902 902 902 902 9021 Этнический 902 902 902 Этнический 9022|||||
| 5 | Арабский | Этнический | ||||
| 6 | Восходящий Мелодический Минор / Джаз Минор | Джаз, Режимы Мелодического Минора | ||||
| 7 | Другое | ПелогЭтнический | ||||
| 9 | Доминантный бибоп | Джаз | ||||
| 10 | Бибоп Дориан / Минор | Джаз | ||||
| 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 9022 Бибоп Мажор | Джаз | |||||
| 13 | Бибоп Мелодический Минор | Джаз | ||||
| 14 | Блюз | Общий | ||||
| 15 | Блюз Мажор | Джаз | ||||
| 16 | Блюз 21 Минор 9021 9021 Этнический 9022 902 902 902 9021 Этнический 902 | |||||
| 18 | Хроматический | Другой | ||||
| 19 | Дориан | Режимы | ||||
| 20 | Двойной гармонический мажор / Византийский 21 / Арабский 902 902 Этнический 9021 902 902 902 Этнический 9021 9021 Этнический 9021 902 9021 Этнический 9021 902 902 902 902 | |||||
| 22 | Enigmatic | Другое | ||||
| 23 | Half-Whole / Dominant Diminished | Jazz | ||||
| 24 | Harmonic 21 | 902Minor21 | 902 Обычный||||
| 26 | Гавайский 902 22 | Этническая | ||||
| 27 | Хираджоши | Этническая, японская | ||||
| 28 | Венгерская минорная шкала / двойная гармоническая минорная / цыганская малая | Этническая | 902/902 Джаз||||
| 30 | In / Sakura Pentatonic | Этническая, японская | ||||
| 31 | Insen | Этническая, японская | ||||
| 32 | 902Ionian | 902 902Этническая, японская | ||||
| 34 | Локрийская | Режимы | ||||
| 35 | Локрийский ♮ 2 / Half-Diminished / Aeolocrian ‘ | Джаз, Мелодические режимы 21 | ||||
| 37 | Lydian Augmented / Lydian ♯5 | Jazz, Modes of Melodic Minor 90 222 | ||||
| 38 | Lydian Dominant / Lydian ♭ 7 / Acoustic / Mixolydian ♯4 / Overtone / Lydomyxian ‘ | Jazz, Modes of Melodic Minor | ||||
| 39 | Major | General | Common | Common | Major | Этническая |
| 41 | Мелодическая минор | Общая | ||||
| 42 | Минор Пентатоника | Общая | ||||
| 43222 | ||||||
| 4322 | ||||||
| 4322 Mixolydian 6 / Melodic Major / Hindu / Myxaeolian ‘ | Джаз, Мелодический минор | |||||
| 45 | Натуральный минор | Общий | ||||
| 46 | 902 902 Этнический Неаполитанец МалыйЭтнический | |||||
| 48 | Восточный | Этнический | 902 17||||
| 49 | Персидский | Этнический | ||||
| 50 | Фригийский | Режимы | ||||
| 51 | Фригийский ♮ 6 / дорийский ♭ 2 / Маззский 2 / Ассирийский21 | фригидорский 90252 | Фригийский доминант | Этнический | ||
| 53 | Прометей | Другой | ||||
| 54 | Румынский мажор | Этнический | 9022||||
| Этнический | ||||||
| Этнический | ||||||
| Super Locrian / Altered (Dominant) ‘ | Джаз, режимы мелодического минора | |||||
| 57 | Тритон | Другой | ||||
| 58 | Двухполутонный тритон | Другой | Другой | Украинский дорийский / румынский минор | Этнический | |
| 60 | Весь тон 9022 2 | Другое | ||||
| 61 | Йо | Этнический, японский |
Музыкальные весы 101: Музыкальные весы для начинающих
В теории музыки гаммы — одна из самых важных вещей, которую вы должны выучить. Это основа музыки, и изучение шкал и диаграмм существенно улучшит ваше сочинение песен и способность изучать новую музыку. Вот почему я предоставлю вам определение музыкальной гаммы, а также инструменты для их самостоятельной работы.
Это основа музыки, и изучение шкал и диаграмм существенно улучшит ваше сочинение песен и способность изучать новую музыку. Вот почему я предоставлю вам определение музыкальной гаммы, а также инструменты для их самостоятельной работы.
Большинство из нас уже подсознательно знает музыкальные гаммы и может петь их, поскольку мы приобщаемся к музыке с юных лет. Если бы кто-то спел пару нот и попросил вас спеть следующую, вы бы смогли это сделать, но, возможно, не обладали знаниями.
В этой статье мы рассмотрим различные гаммы в музыке, как они работают и как использовать гаммы для создания музыки и улучшения написания песен!
Что такое музыкальные весы?Музыкальные гаммы — это группы нот, которые приятно звучат при воспроизведении в последовательности или вне ее, восходящей или нисходящей. Если вы когда-нибудь слышали, чтобы кто-то разогревал вокал, обычно они поют гаммы. Это определение можно рассматривать как грубый способ объяснения этой темы, однако оно направит вас на правильный путь исследования.
Более простое определение музыкальной гаммы состоит в том, что ноты каждой музыкальной гаммы можно рассматривать как алфавиты языка. Так же, как в разных языках разные алфавиты или буквы, каждая музыкальная гамма включает разные ноты или буквы.
В музыке есть много разных гамм. Например, в музыке наиболее распространены мажорная и минорная гаммы. Мы начнем с самой базовой музыкальной гаммы, известной как мажорная гамма.
Крупные весы :Первый шаг к построению мажорной гаммы — записать первые 7 букв алфавита, начиная с A (A B C D E F G).Давайте посмотрим на нашу первую крупную гамму, начиная с ноты C. Для этого все, что вам нужно сделать, это переписать тот же порядок нот, но начать с C (C D E F G A B).
Если вы когда-нибудь играли на пианино, вы можете заметить, что это те же ноты, что и белые клавиши. Итак, если вы сыграете все белые клавиши от C до B, вы услышите мажорную гамму. Это отличный способ сыграть свою первую из многих музыкальных гамм на фортепиано!
Это отличный способ сыграть свою первую из многих музыкальных гамм на фортепиано!
Итак, это была наша первая мажорная гамма. Поскольку мы начинаем с ноты C, она будет называться гаммой C Major.Нота в начале музыкальной гаммы обычно определяет ее названия. В данном случае это была мажорная гамма, начинающаяся с до мажор.
Теперь вы, должно быть, думаете: «А что, если я начну ту же шкалу с другой буквы, например G? Будет ли это гамма соль мажор? »Отличная идея, но не все так просто. Но вы на правильном пути!
Как разработать любой крупный масштаб :Теперь, когда мы установили, что гамма до мажор состоит из 7 нот, начиная с до и заканчивая си, давайте продвинемся вперед и разберемся, как работать с любой мажорной гаммой.
Мажорные гаммы следуют этой схеме в отношении прыжков между нотами:
Целое, Целое, Половинное, Целое, Целое, Целое, ПоловинноеТоном называется целый шаг. На пианино это означает перемещение вверх на 2 клавиши или «полшага» (включая черные ноты). Итак, пример целого шага от C до D, потому что я перехожу на один уровень вверх на C #, а затем снова на D.
Полутон называется полутоном. На пианино это означает перемещение на 1 клавишу вверх (включая черные ноты).Пример полушага взят из C — C #, потому что я просто перемещаюсь на одну клавишу вверх от белого к черному.
Если вы посмотрите на шкалу до мажор и сосчитаете изображение фортепиано, используя шаблон ниже, вы увидите, что он следует по следующей схеме шагов:
C (W) D (W) E (H) F (W) G (W) A (W) B (H) C
Не забывайте также, что на некоторых клавишах есть лыски (b) и Sharps (#).Это черные ноты на фортепиано, если они слева от ноты, это бемоль. Если он справа от ноты, это диез. Итак, если вы разрабатывали гамму си-бемоль мажор, по-прежнему применяется тот же паттерн.
Bb (W) C (W) D (H) Eb (W) F (W) G (W) A (H) Bb
Альтернативный метод: разработка крупных масштабов
Если это не сидит у вас в голове — не нужно паниковать.В качестве альтернативы существует метод, известный как «числовая» система. Вот простые шаги:
- Дайте номер каждой ноте в гамме — давайте начнем с до мажор (например, C = 1, D = 2 и т. Д.).
- Перезапустите гамму, начиная с 5-й ноты — в данном случае это G. Вот как это будет выглядеть: G A B C D E F. Вот как мы будем работать с гаммой соль мажор.
- Присвойте номера этой шкале (G = 1, A = 2 и так далее)
- Сделайте седьмую ноту (в данном случае F) диезом (#).Это означает, что гамма G Major будет G A B C D E F #.
Вы можете продолжать делать эти шаги, чтобы проработать любой мажорный масштаб! Если вы уже узнали о Пятом круге, вы можете заметить, что он работает точно так же. Если вы еще не узнали об этом, обязательно ознакомьтесь с нашим руководством по Пятому кругу, так как оно может помочь вам изучить эту технику нумерации более наглядно.
Музыкальные весы мира:Мажорные гаммы — не единственные доступные музыкальные гаммы.Для создания различных музыкальных настроений используются разные музыкальные гаммы. Однако эти новые шкалы очень легко построить, изменив основную шкалу. Продолжайте читать, чтобы увидеть список музыкальных гамм! Это некоторые из «общих» гамм, используемых в современной музыке.
(Натуральные) Мелкие весы:Это первая немажорная шкала, о которой мы будем говорить. Есть несколько способов составить эту шкалу. Самый простой способ — взять любую крупную шкалу и переписать ее, начиная с 6-й степени (примечание).
В гамме до мажор у нас есть ноты C D E F G A B, что делает A шестой нотой. Теперь давайте перепишем гамму, начиная с A. Мы получим A B C D E F G, который будет называться A Natural Minor.
То, что мы только что сделали, это игра мажорной гаммы 6-й ступени, чтобы получить естественный минор 6-й ноты. Другой пример этого может быть в тональности ре мажор. Масштаб D мажор — D E F # G A B C # D. Шестая нота — B, и если мы ее переписываем, у нас будет B C # D E F # G A B.Это называется гаммой B Natural Minor и т. Д.
Гармонический минор:Шкала Harmonic Minor очень похожа на гамму Natural Minor, так как состоит из тех же нот, за исключением одной разницы. 7-я нота, которая обычно является плоской нотой в натуральном миноре, будет возвращена в нормальное состояние или останется такой же, как и в мажорной гамме.
В тональности C гармоническая минорная гамма будет выглядеть так: C D Eb F G Ab B
Мажорная пентатоника:Как следует из названия, «пентатонические» гаммы включают только 5 нот вместо 7.На самом деле, мажорные пентатонические гаммы — это просто мажорная гамма с 5 нотами. Мажорная пентатоника — это ноты (или «градусы») 1, 2, 3, 5, 6 обычной мажорной гаммы, что делает ее просто мажорной гаммой без степеней 4 и 7.
Например, в тональности C мажорной пентатоникой будет C D E G A.
Минорная пентатоника:Эта пентатоника очень похожа на мажорную пентатонику, так как она также состоит из 5 нот вместо 7. Минорные гаммы пентатоники находятся в естественной минорной гамме.
Итак, возьмите шкалу Natural minor, которую вы можете вычислить, следуя нашим советам выше. Минорная пентатоника — это просто ноты (или «градусы») 1, 3, 4, 5, 7 естественной минорной шкалы.
Например, в тональности C минорная пентатоника будет иметь вид A C D E G.
Blues Масштаб:Шкала блюза состоит из 6 нот, и по сути это минорная пентатоника с дополнительной нотой. Эта гамма обычно используется в блюзовой музыке, как следует из названия, но ноты можно играть в любом стиле, в зависимости от игрока.Вот формула шкалы Блюза.
В тональности до мажорная гамма блюза будет выглядеть так: C D Eb E G A
Вы сделали это!
Музыкальные гаммы можно рассматривать как музыкальные языки, состоящие из разных нот. Эти гаммы позволяют музыкантам создавать мелодии, риффы, соло или даже импровизировать, звуча при этом мелодично или связно.
Существует намного больше гамм, чем указано в этой статье, однако их должно быть достаточно, чтобы вы начали понимать музыку в более глубоком смысле.
В конце концов, насколько правила помогут, лучше всего найти свои собственные новые методы и поэкспериментировать с ними.
| cta-link type = ’artist-development’ |
Надеюсь, эта информация даст вам понимание того, как разрабатывать мажорные и минорные гаммы для любой тональности. Если вы нашли это полезным, не стесняйтесь поделиться с кем угодно, начинающим теорией музыки, или тем, кто хотел бы получить дополнительную информацию об основах музыки, чтобы поддержать их артистизм.
Music Gateway всегда готов помочь артистам, будь то такие статьи, как эта, Возможности синхронизации или музыкальное продвижение. Не верьте нам на слово, попробуйте бесплатно сегодня, зарегистрировавшись или нажав кнопку ниже.
Ваша музыкальная карьера
Вперед.
«Чтобы добиться успеха в этом бизнесе, нужно убедиться, что у вас есть все, что нужно для успеха ».
Чего вы можете ожидать от наших информационных бюллетеней:- Новости отрасли и советы
- Возможность представить свою музыку и сотрудничать с другими
- Бесплатное программное обеспечение и ресурсы
- Бесплатное членство в Music Gateway
Вы уверены, что это правильный адрес электронной почты?
Спасибо! Информационные бюллетени будут отправлены по адресу:.Это правильный адрес электронной почты? Если нет, то можете поправить. Нежелательная почта? Черт возьми, мы тоже это ненавидим!
Нажмите здесь, чтобы получать нашу рассылку!
Новости и возможности
Спасибо! Информационные бюллетени будут отправлены по адресу:.Это правильный адрес электронной почты? Если не, вы можете это исправить.
Попробовать бесплатно
Все, что нужно для продвижения и заработка.
Зарегистрируйтесь сегодня для получения полностью бесплатной 14-дневной пробной версии Music Gateway.- Лицензия на музыку для фильмов, телевидения и рекламы
- Управляйте музыкой и метаданными
- Отправлять музыку лейблам и издателям
- Создание плейлистов для демонстрации представителям A&R
- Сотрудничать с другими и предлагать работу
- …и многое другое!
Скачать бесплатно
Загрузите БЕСПЛАТНЫЙ набор художников .
Получите бесплатный набор артистов, когда подпишетесь на полностью бесплатная 14-дневная пробная версия Music Gateway.- 5GB + образцов
- Плагины VST
- Производственные файлы и шаблоны Midi
- Отраслевые руководства и инструкции
- Список кураторов Spotify
- …и многое другое!
Возможно, вам будут интересны некоторые из наших услуг…
Теория
— В чем разница между режимом и шкалой?
Я изучаю композицию в Калифорнийском университете в Лос-Анджелесе и сейчас пишу свою диссертацию, которая на одном уровне имеет много общего с модами — так что сейчас я много думаю об этом (что привело меня на этот сайт). Вот мои мысли:
Ответ Роберта Финка (см. Выше) — отличный ответ.Это тип ответа, который вы получите от того, кто занимается музыкой в течение долгого времени, тип ответа, который вы могли бы ожидать от музыковеда. Частично я обвиняю учебники истории музыки в путанице, связанной с «режимом», потому что в учебнике приведенный выше ответ действительно существует, но распределен по многим главам, и поэтому довольно сложно соединить точки, на самом деле я думаю, что многие студенты-музыкальные студенты имели бы Трудно дать точное определение «режиму».
Это может помочь сначала объяснить греческую систему ладов (тонои), поскольку, насколько нам известно, именно здесь все началось (по крайней мере, для Западной Европы).Насколько я понимаю, древние греки представляли лады как серию нисходящих тетрахордов («нисходящую последовательность четырех тонов»). Мы, конечно, думаем о весах и модах как о восходящих, что является результатом неправильного понимания средневековыми учеными древнегреческих текстов. Было 3 разных тетрахорда, которые они назвали «родами»: хроматический, диатонический и энгармонический. Я сосредоточусь на «диатонике», поскольку именно тетрахорд больше всего напоминает нашу современную гамму. Диатоника состояла из двух нисходящих целых шагов, за которыми следовала половина.Сегодня мы можем думать об этом как об E-D-C-B. Согласно «Гармоникам» Птолемея, которые, возможно, являются наиболее точным описанием мод (никто на самом деле не понял это на 100%), эти тетрахорды будут соединены, чтобы сформировать моду (точно так же, как они это делали в Средние века и в Средние века). Ренессанс). Вот древнегреческий дорийский лад: нисходящий E-D-C-B-A-G-F-E: два нисходящих диатонических тетрахорда, разделенных целым шагом. Вы можете видеть, насколько оторвались средневековые ученые, когда они переводили греческий (не то чтобы это была их вина, они старались), наш восходящий дорийский язык, D-E-F-G-A-B-C- (D) звучит совсем иначе, чем их дорийский.Греческая система режимов была очень сложной, поэтому я остановлюсь на времени и пространстве.
Суть предыдущего (и несколько утомительного — извините) абзаца заключается в том, что, возможно, лучший способ думать о «режиме», как он использовался на протяжении тысячелетий, — это думать о трихордах, тетрахордах, пентахордах или гексахордах, которые связаны между собой интервал (например, целый или полушаговый) или это перекрытие для создания «крупномасштабной структуры». Таким образом, дориан, как указал Роберт Финк, — это два перекрывающихся гексахорда, но на самом деле они считаются двумя тетрахордами:
перекрывающихся шестигранников: [C-D-E-F- {G-A] B-C-D-E}, что приводит к
два тетрахорда: D-E-F-G -A-B-C-D. В конце 19-го и начале 20-го веков композиторы начали использовать «синтетические лады» (потому что они не являются производными от системы mojor / minor / modal). Первые были цельнотоническими и октатоническими (8-нотные). Целый тон создается путем соединения только целых шагов, например: C-D-E-F # -G # -A # -C. Octatonic создается путем соединения целых шагов и полушагов или наоборот, например: C-C # -D # -E-F # -G-A-Bb-C. Но, как и греческий и средневековый лады, вы также можете думать о них как о связанных трихордах или тетрахордах:
полнотональных трихордов: [C-D-E] — [F # -G # -A #]
Октатонический как трихорд или тетрахорд: [C-C # -D #] — [E-F # -G] — [A-Bb-C] или [C-C # -D # -E] — [F # -G-A-Bb] — [C-C # и т. Д..]
Обратите внимание, что в обоих случаях сохраняется шаблон интервала полушага (W) и полутона (H): полнотонный — [W, W] -W- [W, W], октатонический — [H, W] — H- [H, W] -H- [H, W] [В, Ш, В] -З- [В, Ш, В]. (Примечание: два «синтетических режима» выше симметричны, поэтому их можно разделить любым способом и при этом сохранить четкий интервальный шаблон — это то, что делает их такими интересными и такими скучными).
Гексатонический режим последовал несколько позже и создается чередованием полушагов и минорных третей: C-C # -E-F-G # -A-C и может быть разделен следующим образом: [C-C # -E-F #] — [G # -A-C-C #] или [H, m3, H] -m3- [H, m3, H] -m3- [H, m3, H] и т. Д..
Позднее, начиная с 1920-х / 30-х годов, такие композиторы, как Бела Барток, Оливье Мессиан, Витольд Лютославски и Анри Дютийё (среди многих других) создали свои собственные «лады». Лютославский, например, сделал бы что-то вроде этого: P5, M3, m2, P5, M3, m2 и т. Д.
Итак, я думаю, что в самом общем смысле режим — это «некоторый образец интервалов, которые могут или не могут быть разделены другим интервалом», как в примере Лютославского, или даже что-то столь же сложное, как:
[P5, M3, M2] -tt- [P5, M3, M2] -m2- [P5, M3, M2] -tt- [P5, M3, M2] -m2 и т. Д.
По моему опыту, большинство композиторов, с которыми я говорю сегодня, воспринимают «моду» как концепцию. Причина, по которой мы думаем о «дорианской моде» как о шкале до мажор, которая начинается и заканчивается на D, заключается в том, что мы играем в исторический «телефон» (например, в детскую игру) в течение 2500 лет; греки говорят в один конец телефона в 500 г. до н.э. «вот дорий», а 1000 лет спустя западноевропейцы говорят, что это фригийский, и называют что-то еще дорианское, еще 1500 лет спустя русские и французские импрессионисты и джазовые парни говорят: «помните те старые гаммы. которые начинались с разных степеней до мажор, звучало круто »
Итак, да, в теории джаза уместно называть все белые ноты от D до D «дорианской модой», потому что они так думали об этом, но неуместно думать об этом таким образом, если вы учитесь древнегреческая или средневековая музыка — все дело в контексте.
И, наконец, мысль о масштабах и моде. Вот некоторые обобщения, которые до некоторой степени являются моими мнениями или, скорее, моим представлением о масштабе и режиме:
шкалы имеют начало и конец (вроде). До мажор основан на функциональной западной тональной гармонии, это означает, что когда вы поднимаетесь по шкале и достигаете B, вы почти достигаете «конца» шкалы, «говоря гармонично». Синтаксически говоря, B — это последняя глава, а C — это «и они жили долго и счастливо». Если вы нажмете B и остановитесь на этом, публика почувствует себя очень неуютно, думайте об этом как о «гармоничном грани».»
моды, если не проходить через 19 век, западноевропейская модель функциональной гармонии (как в джазе) не имеет начала и конца, они могут идти в любом направлении вечно.
Весыимеют функциональные степени. То же самое и с режимами, но система несколько шире проработана с масштабами. У ладов есть финальный и доминантный, а также мелодические паттерны, как и у гамм, но у гамм есть тоника и доминанта, И субдоминантный, срединный, субмедиантный, супертонический и ведущий тон.
Режимыимеют тенденцию придавать больший вес интервалам, шкалам степеней шкалы и гармонической функции.
Ок. Я задолбался. Надеюсь, это поможет и не усложнит ситуацию. Это определенно помогло мне прояснить мои мысли о «режиме против масштаба», прежде чем мне пришлось вставить их в раздел моей диссертации :).
На самом деле, есть еще один способ думать о режиме, который представляет собой образ мышления 20-го века, который создает режимы путем «циклического вращения» или «вращения» по всем степеням данной шкалы.Это не следует путать с приведенным выше объяснением, они связаны, но разные.
Традиционно большинство людей думают о ладах как о шкале, которая начинается с другой ступени основной шкалы, отличной от тоники, поэтому ступень шкалы 2 = дорийский, 3 = фригийский, 4 = лидийский, 5 = миксолидийский, 6 = эолийский, и 7 = локрийский. Когда вы делаете это, вы «проходите цикл» через все ступени большой шкалы. Эта идея также может быть распространена на другие гаммы, такие как гармонический минор и пентатоника.Таким образом, у вас может быть пентатоника 1 (мажор), пентатоника 2, пентатоника 3 (минор), пентатоника 4 и пентатоника 5.
С симметричными гаммами, такими как полнотонный, октатонический, гексатонический (и все «режимы ограниченного транспонирования» Мессиана, некоторые из которых упомянуты выше), нет смысла думать о них таким образом, поскольку по большей части, начало с другой «ступени шкалы» приведет к повторению исходной шкалы, то есть: весь тон всегда будет просто отображаться на себя, если вы начнете с любой «ступени шкалы», октатоника имеет 2 режима, весь / половина или половина / весь и для гексатоники ситуация такая же.
Однако, если вы создаете «синтетический режим», который не является симметричным, то можно думать о нем так же, как вы могли бы думать о мажорной гамме до, и вращать различные режимы так же, как вы можете прокрутите все «режимы» до мажорной гаммы.
Например:
Вот мой готовый режим — m2, m2, m3, M3
Это даст вам, начиная с C: C, C #, D, F, A, A #, B, D, F #, G, G #, B, D # и т. Д.
режим 1: C, C #, D, F, A, A #, B, D, F #, G, G #, B, D #
режим 2: C #, D, F, A, A #, B, D, F #, G, G #, B, D #, E
режим 3: D, F, A, A #, B, D, F #, G, G #, B, D #, E, F
и др.
Разница в порядке интервалов, не более:
режим 1: m2, m2, m3, M3
режим 2: m2, m3, M3, m2
режим 3: м3, м3, м2, м2
Итак, режим 1 складывает небольшие интервалы слева от тетрахорда, режим 2 размещает их по обе стороны, а режим 3 складывает их слева.
Я считаю, что это мало что значит, если вы не можете применить какую-то функциональную гармонию к различным режимам, как это сделали музыканты с различными режимами импрессионизма / джаза в 20-м веке.В противном случае это просто установленные классы.
теория — Как узнать, в каком масштабе или в какой тональности композиции (текст и пение) эта песня?
Во-первых, в лирике нет ключа, это просто слова, как стихотворение.
Мелодия не имеет ключа. Это может означать ключ, но это открыто для интерпретации и мнения.
Например, рассмотрим первые семь нот «Мерцай, мерцай, маленькая звездочка».
(начиная с ноты C)
C C G G A A G
Эти примечания появляются в:
(эти списки несколько сокращаются, если анализировать всю мелодию)
Как видите, существует множество вариантов и буквально тысячи способов гармонизировать мелодию. Вы используете свой слух, чтобы направлять вас к подходящим аккордам для вашей мелодии.
Первоначальный композитор решил сделать это следующим образом:
Ноты мелодии: C C G G A A G Аккорды: Cmaj Fmaj Cmaj
Мажор, очень созвучный, простой I IV I прогрессия, идеально подходит для детской песни.
Вот несколько альтернатив:
Ноты мелодии: C C G G A A G Аккорды: Am Am7 D7 G Ноты мелодии: C C G G A A G Аккорды: Am Em Dm Cmaj Ноты мелодии: C C G G A A G Аккорды: F Gm Am Em Ноты мелодии: C C G G A A G Аккорды: Cm Gm F7 Bbmaj6 Ноты мелодии: C C G G A A G Аккорды: Dbmaj7 Bbm9 Edim Am7 Fmaj9 D7 G6 / 9
Сыграйте их и послушайте, как они меняют характер мелодии.
Все мои примеры полностью основаны на тонах аккорда: Нота мелодии встречается внутри аккорда. Это надежный способ найти аккорды, подходящие для вашей мелодии. Это (или, скорее, может быть) путь к очень скучным песням, поскольку для напряжения и драмы требуются неаккордовые тона.
Поскольку вы пишете свои собственные мелодии, у вас, вероятно, есть какое-то предвзятое представление (возможно, подсознательное) о том, как его следует гармонизировать. Попробуйте:
- Выучите мелодию на своем инструменте.
- Определите ключевую ноту (ноту, которая «чувствует себя как дома» и дает общее разрешение). Примечание, которое дает ощущение окончания, как точка для предложения. окончание на любых других нотах звучит как нефини
Поэкспериментируйте с аккордами из выбранной вами тональности. Аккорды I IV и V могут гармонизировать любую диатоническую мелодию, поэтому начните с них. Работайте над этим, пока не найдете последовательность аккордов, которая, по вашему мнению, подходит.
А главное УЧИТЬ ПЕСНИ! Как вы можете рассчитывать на написание отличных песен, если вы не можете определить, что делает отличная песня ?! Изучите и проанализируйте песни, которые вам нравятся, чтобы увидеть, как мелодия и гармония сочетаются друг с другом и что именно заставляет вас полюбить эту песню.
4.8 Неосновные и неосновные весы
Звуки — обычные, повседневные «шумы» — бывают всех мыслимых высот и групп высот. Фактически, суть шума, «белый шум», заключается в каждой высоте звука одновременно, так что не слышно никакой конкретной высоты звука.
Одна из вещей, которая делает музыку приятной для прослушивания и легкой для «понимания», — это то, что используются только некоторые из всех возможных высот. Но не во всех музыкальных произведениях используется один и тот же набор высоты звука. Чтобы узнать, какие ноты могут использоваться в музыкальном произведении, музыканты изучают гаммы.
Набор ожидаемых высот для музыкального произведения можно упорядочить в масштабе . В шкале высоты тона обычно располагаются от самого низкого до самого высокого (или от самого высокого к самому низкому), в шаблоне, который обычно повторяется в каждой октаве.
ПримечаниеВ некоторых музыкальных жанрах ноты определенной гаммы — единственные ноты, разрешенные в данном музыкальном произведении. В других музыкальных традициях ноты вне гаммы (случайные) разрешены, но обычно встречаются гораздо реже, чем ноты гаммы.
Набор используемых звуков или нот и их взаимосвязь друг с другом оказывает большое влияние на то, как звучит музыка. Например, на протяжении веков большая часть западной музыки была основана на мажорной и минорной гаммах. Это одна из вещей, которая делает ее мгновенно узнаваемой как западную музыку. С другой стороны, большая часть (хотя и не вся) музыки Восточной Азии на протяжении многих веков была основана на пентатонических гаммах, что придавало ей совершенно иной оттенок, который также легко распознать.
Здесь представлены некоторые из наиболее часто используемых гамм, которые не являются мажорными или минорными. Пентатонические гаммы часто ассоциируются с Восточной Азией, но многие другие музыкальные традиции также используют их. Блюзовые гаммы, используемые в блюзе, джазе и других афроамериканских традициях, выросли из компромисса между европейскими и африканскими гаммами. Некоторые гаммы, которые кажутся «экзотическими» для западного уха, взяты из музыкальных традиций Восточной Европы, Ближнего Востока и Западной Азии. Микротоны можно найти в некоторых традиционных музыкальных произведениях (например, в индийской классической музыке) и в некоторых произведениях современного искусства.
ПримечаниеНекоторые музыкальные традиции, такие как индийские и средневековые европейские, используют лады или раги, которые не совсем то же самое, что гаммы. См. Режимы и Раги.
Западная музыкальная традиция, развившаяся в Европе после средневековья, основана на мажорной и минорной гаммах, но есть и другие гаммы, которые являются частью этой традиции.
В хроматической шкале каждый интервал составляет полшага. Эта гамма дает все резкие, плоские и естественные ноты, обычно используемые во всей западной музыке.Это также 12-тональная шкала , используемая композиторами двадцатого века для создания своей атональной музыки. Молодым инструменталистам рекомендуется попрактиковаться в игре на хроматической гамме, чтобы убедиться, что они знают аппликатуры для всех нот. Послушайте хроматическую гамму.
Рисунок 4.65. Хроматическая шкала
Хроматическая гамма включает в себя все тональности, обычно встречающиеся в западной музыке. Обратите внимание, что из-за энгармонического написания многие из этих высот могут быть написаны по-другому (например, с использованием плоских букв вместо диеза).В целой шкале тонов каждый интервал представляет собой целый шаг. И в хроматической, и во всей шкале тонов все интервалы одинаковы. В результате получаются гаммы без тонального центра; ни одна нота не кажется более или менее важной, чем другие. По этой причине в самой традиционной и популярной западной музыке используются мажорные или минорные гаммы, а не хроматические или целые тональные гаммы. Но композиторы, которые не хотят, чтобы в их музыке был тональный центр (например, многие композиторы «современной классической» музыки), часто используют эти гаммы.Слушайте всю шкалу тонов.
Рисунок 4.66. Шкала всего тона
Поскольку все интервалы одинаковы, не имеет большого значения, где вы начинаете хроматическую или целую шкалу тонов. Например, эта гамма будет содержать одни и те же ноты независимо от того, начинаете ли вы ее с C или E.
Упражнение 4.8.1. (Перейти к решению)
В основном имеется только одна хроматическая гамма; вы можете начать его с любой ноты, но в конечном итоге высота звука будет такой же, как и в любой другой хроматической гамме.В основном есть две возможные шкалы полных тонов. Начиная с a b, напишите целую шкалу тонов, в которой используются звуки, отличные от показанной на рис. 4.66. Если вам нужна служебная бумага, вы можете скачать этот PDF-файл.
В западной музыке есть двенадцать высот в каждой октаве. (Тринадцатая нота начинает следующую октаву.) Но в музыкальном произведении часто используются только семь из этих нот, семь нот мажорной или минорной гаммы.
В шкале пентатоники используются только пять возможных высот в октаве.(Таким образом, гамма будет повторяться, начиная с шестого тона.) Наиболее известные пентатонические гаммы используются в большей части музыки Восточной Азии. Возможно, вы знакомы со шкалой на рис. 4.67 как шкалой, которая получается при нажатии всех «черных клавиш» на клавиатуре пианино.
Рисунок 4.67. Знакомая шкала пентатоники
Это пентатоника, которую вы получаете, когда играете на «черных клавишах» пианино.
Слушайте пентатонику в черном ключе.Как и другие гаммы, эта пентатоническая гамма переносима; вы можете переместить всю шкалу вверх или вниз на полшага, большую треть или любой интервал, который вам нравится. Шкала будет звучать выше или ниже, но в остальном она будет звучать так же, потому что образец интервалов между нотами (полушаги, целые шаги и второстепенные трети) одинаков. (Для получения дополнительной информации об интервалах см. Полушаги, Целые шаги и Интервал. Для получения дополнительной информации о паттернах интервалов внутри гамм см. Главные и Минорные гаммы.) Теперь послушайте транспонированную пентатоническую гамму.
Рисунок 4.68. Транспонированная пентатоническая шкала
Но это не единственный возможный тип пентатоники. Любая гамма, в которой используются только пять нот в пределах одной октавы, является пентатонической гаммой. Следующая пентатоника, например, не просто еще одна транспозиция пентатонической гаммы «черный ключ»; рисунок интервалов между нотами другой. Послушайте эту другую пентатонику.
Рисунок 4.69. Шкала разной пентатоники
Эта пентатоническая шкала не является транспонированной версией рисунка 4.67. У него другой набор интервалов.Дело здесь в том, что музыка, основанная на пентатонической шкале на рисунке 4.67, будет звучать очень иначе, чем музыка, основанная на пентатонической шкале на рисунке 4.69, потому что отношения между нотами различны, так же как музыка в минорной тональности заметно отличается от музыки в минорной тональности. музыка в мажорной тональности. Таким образом, существует довольно много различных возможных пентатонических гамм, которые будут производить узнаваемый «уникальный звук», и многие из этих возможных пяти нотных гамм были названы и используются в различных музыкальных традициях по всему миру.
Упражнение 4.8.3. (Перейти к решению)
Чтобы получить представление о концепциях этого раздела, попробуйте составить несколько коротких пьес, используя шкалы пентатоники, представленные на рис. 4.67 и 4.69. Вы можете использовать более одной октавы каждой гаммы, но используйте только одну гамму для каждой пьесы. Когда вы сочиняете, прислушивайтесь к тому, как ограничения использования только этих пяти нот с этими отношениями высоты тона влияют на вашу музыку. Посмотрите, сможете ли вы воспроизвести композицию, изображенную на рис. 4.67, в другой тональности, например, используя масштаб на рис. 4.68.
Более или менее деление октавы
Любая гамма будет содержать определенное количество нот в октаве. Для мажорной и минорной гаммы есть семь нот; для пентатоники — пять; для хроматической гаммы — двенадцать. Хотя некоторые подразделения более распространены, чем другие, можно вообразить любое разделение, и многие из них используются в различных музыкальных традициях по всему миру. Например, классическая музыка Индии распознает двадцать две различных возможных высоты звука в пределах октавы; каждая рага использует пять, шесть или семь из этих возможных звуков.(Подробнее об этом см. Индийская классическая музыка: настройка и раги.) В Африке есть некоторые традиции, в которых используется шесть или восемь нот в октаве. Слушайте одну возможную восьмитональную или октатоническую гамму.
Рисунок 4.70. Октатоническая шкала
Многие незападные традиции, помимо использования разных гамм, также используют разные системы настройки; интервалы в шкалах могут включать четвертных тонов, (половина полутона), например, или другие интервалы, которые мы не используем.Даже попытка записать их в общих обозначениях может ввести в заблуждение.
Микротоны — это интервалы меньше полушага. Помимо того, что они необходимы для описания гамм и систем настройки многих незападных традиций, они также использовались в современной западной классической музыке, а также в афроамериканских традициях, таких как джаз и блюз. На момент написания этой статьи Фонд Гюйгенса-Фоккера был хорошим местом для начала поиска информации о микротональной музыке.
Создание блюзовой гаммы
Весы блюза тесно связаны с гаммами пентатоники. (Некоторые версии являются пентатоническими.) Переставьте шкалу пентатоники на рис. 4.68 выше так, чтобы она начиналась с C, и добавьте фа-диез между F и G, и вы получите обычно используемую версию гаммы блюза. Послушайте эту гамму блюза.
Рисунок 4.71.
Блюзовые гаммы тесно связаны с пентатоническими гаммами.
Во многих музыкальных традициях гаммы не используются.Наиболее знакомы западному слушателю средневековые песнопения и классическая музыка Индии. В этих и других модальных традициях правила построения музыкального произведения сильно отличаются от правил для музыки, основанной на гамме. Пожалуйста, смотрите Режимы и Раги для получения дополнительной информации.
Есть много-много других возможных гамм, которые не являются частью системы мажор-минор. Некоторые, например пентатонические и октатонические гаммы, содержат меньше или больше нот на октаву, но многие имеют семь тонов, как и мажорная гамма.Шкала может быть выбрана или построена композитором для определенных интригующих характеристик, для типов мелодий или гармоний, которые позволяет гамма, или просто для интересного или приятного звучания музыки, созданного с использованием гаммы.
Например, один класс гамм, который интригует некоторых композиторов, — это симметричных гамм . Хроматическая шкала и целые шкалы тонов попадают в эту категорию, но могут быть построены и другие симметричные шкалы. Например, уменьшенная шкала не только обладает «симметричным» качеством; это также очень полезная гамма, если, например, вы импровизируете джазовое соло поверх уменьшенных аккордов.
Рисунок 4.72. Масштаб уменьшенный
Подобно хроматической шкале и шкале цельных тонов, уменьшенная шкала «симметрична».
Некоторые гаммы основаны на музыке других культур и используются, когда композитор хочет вызвать музыку из другого места или времени. Эти гаммы часто заимствуются из незападных традиций, но затем используются способами, типичными для западной музыки. Поскольку они обычно игнорируют строй, мелодические формы и другие эстетические принципы традиций, из которых они заимствованы, такое использование «экзотических» гамм не следует рассматривать как точное представление этих традиций.Однако в мировой музыке есть примеры, в которых незападная гамма или мода используются аутентичным образом. Хотя существует общее согласие относительно названий некоторых обычно используемых «экзотических» шкал, они совсем не стандартизированы. Часто название шкалы просто отражает то, как она звучит для человека, использующего ее, и одно и то же имя может быть применено к разным шкалам или разные имена к одной и той же шкале.
Рисунок 4.73. Некоторые «экзотические» весы
Вы можете поэкспериментировать с некоторыми из множества возможных шкал.Послушайте по одной версии каждой из: «уменьшенной» шкалы, «загадочной» шкалы, «румынской» шкалы, «персидской» шкалы и «венгерской крупной шкалы». Чтобы получить еще больше возможностей, попробуйте поискать в Интернете по запросу «экзотические масштабы»; или попробуйте придумать свои собственные гаммы и использовать их в композициях и импровизациях.
Рисунок 4.74. «Загадочная» шкала
Решение упражнения 4.8.1. (Вернуться к упражнению)
Рисунок 4.75.
Вся эта шкала тонов содержит ноты, которых нет во всей шкале тонов на Рисунке 4.66.Решение упражнения 4.8.2. (Вернуться к упражнению)
Рисунок 4.76.
Плоскости в одной гамме — это энгармонические эквиваленты диезов в другой гамме.Предполагая, что октавы не имеют значения — как это обычно бывает в западной музыкальной теории, эта шкала разделяет все свои возможные высоты со шкалой на рисунке 4.66.
Решение упражнения 4.8.3. (Вернуться к упражнению)
Если можете, попросите учителя послушать ваши сочинения.
мажорных гамм: как использовать наиболее важные музыкальные гаммы
мажорные гаммы являются важным строительным блоком всей западной музыки. Это одна из наиболее часто используемых музыкальных гамм.
Сидеть и заниматься большой гаммой — это не для кого-то развлечения, но в будущем это будет вознаграждение.
Зная свои мажорные гаммы изнутри и снаружи, вы сможете ориентироваться во всех аспектах теории музыки.
В этой статье я объясню, что такое мажорные гаммы, и как вы можете начать понимать их и использовать в своей музыке.
Какой крупный масштаб?
Мажорная гамма — это шкала из семи нот, состоящая из серии целых шагов и полушагов. Полушаги существуют между третьей и четвертой, а также седьмой и восьмой ступенями шкалы.
Другое название мажорной гаммы — диатоническая гамма. Это просто означает, что полушаги шкалы максимально растянуты.
Если это звучит сбивающе с толку, не волнуйтесь! В этой статье мы разберем все шаги, полушаги и градусы шкалы.
Приступим.
Как построить крупную шкалу
Глядя на фортепиано, проще всего начать понимать мажорную гамму.
Основная шкала — это шкала из семи нот, состоящая из серии целых шагов и полушагов
Если вы посмотрите на все белые клавиши пианино, вы увидите гамму до мажор.
Шкала до мажор начинается с белой клавиши, которая идет перед двумя черными клавишами. Это первая ступень шкалы.
Прежде чем мы начнем строить мажорную шкалу, вам важно знать целые шаги и полушаги.
Полушаг — это расстояние от одной ноты до следующей. Один полный шаг равен двум полушагам.
Один полушаг — это расстояние от одной ноты до следующей. Один полный шаг равен двум полушагам.
А теперь посмотрите на пианино. Найдите C и используйте следующую формулу, чтобы сыграть до мажорную гамму: w шаг лунки, целый шаг, полушаг, весь шаг, весь шаг, весь шаг, полушаг .
Когда вы играете гамму в соответствии с целыми шагами и половинными шагами, вы также будете проигрывать каждую ступень шкалы от одного до семи.
Поздравляем! Вы только что сыграли до мажор. Эта гамма подскажет вам музыкальный тон до мажор: никаких диезов и бемолей.
Построение основных шкал в других тональностях
Вы сможете построить гамму, начиная с любой ноты, если сможете сделать это в тональности до мажор.
Вы сможете построить гамму, начиная с любой ноты, если сможете сделать это в тональности до мажор.
Когда вы строите мажорную гамму в других тональностях, вы начинаете использовать черные клавиши пианино, чтобы соответствовать формуле мажорной гаммы.
Давайте посмотрим на мажорную гамму ре мажор.
Начните с D и используйте формулу мажорной шкалы
D весь шаг до E, целый шаг до F #, полшага до G, целый шаг до A, весь шаг до B, целый шаг до C #, полушаг до D.
Вы также заметите, что ключевой сигнатурой ре мажор является F # и C #.
Это может занять некоторое время, чтобы привыкнуть, когда вы начнете практиковать это.Со временем вы начнете привыкать к нему.
Через некоторое время вы почувствуете, что это становится более естественным. Применение этой информации к другим областям музыки будет для вас быстрее и проще.
Не бойтесь повторить эту формулу по кругу квинт и отработать каждую тональность.
Режимы большой шкалы
Мажорная гамма также используется для построения музыкальных ладов. Режимы содержат относительную минорную гамму, а также другие часто используемые гаммы.
Все режимы основаны на формуле большого масштаба.
Все режимы основаны на формуле основной шкалы.
Мы называем основную шкалу ионической формой, потому что она начинается с первой ступени шкалы. Остальные шесть ступеней шкалы в основной шкале предоставят вам разные режимы.
Например, если начать гамму до мажор со второй ноты D, получится D дорийская мода: D E F G A B C D.
Продолжите этот паттерн, начав гамму до мажор на любой ноте.Это даст вам различные режимы мажорной гаммы, и вы начнете слышать различные тональные качества, когда играете на них.
Ознакомьтесь с нашим подробным руководством, если вы хотите глубже погрузиться в музыкальные режимы.
Мажорные гаммы в музыке
Мажорная гамма считается основной в западной музыке. Это яркий и стабильный звук, который у нас ассоциируется с приятной музыкой.
Мажорная гамма — это основа функциональной гармонии в музыке.Помните схему тон-полутон, о которой я говорил раньше?
Положение полутоновых интервалов — это то, что создает ощущение напряжения и расслабления в последовательностях аккордов, построенных с нотами в мажорной гамме.
Это может показаться немного теоретическим, но именно по этой причине мажорную гамму можно найти в музыке абсолютно повсюду.
С такой фундаментальной шкалой довольно сложно сказать, как лучше ее использовать. Лучший совет — следить за своими ушами и позволять собственному творчеству руководить вами.
Не зря
Не забывайте мажорную шкалу в своей повседневной практике. Попрактикуйтесь во всех 12 тональностях. Используйте его для создания новых мелодий и гармонии.
Когда у вас в ушах эта гамма, вы будете естественно, когда пойдете создавать свою следующую песню.
типов музыкальных весов: руководство для начинающих
Если вы учитесь играть на музыкальном инструменте, то довольно часто первым делом вы учитесь играть на мажорной гамме, но на самом деле существует множество различных гамм.Некоторые звучат счастливыми, некоторые — грустными, в некоторых — пять нот, а в некоторых — двенадцать.
В этом посте мы собираемся рассказать обо всех типах музыкальных гамм, о теории, лежащей в основе их, а также о том, как их формировать. Давайте начнем.
Что такое шкала в музыке?
Шкала — это группа нот, расположенных в порядке возрастания или убывания высоты тона.
В возрастающей шкале каждая нота по высоте выше, чем последняя, а в нисходящей шкале каждая нота ниже по высоте, чем последняя.
Градусы шкалы
Слово «масштаб» происходит от латинского слова, означающего «лестница».
Итак, вы можете представить себе весы, поднимающиеся по ступеням лестницы, которую представляет посох.
Градусы шкалыУ вас должна быть отметка на каждой строке или на каждой строке.
Каждой ступени шкалы присвоено специальное название:
.- 1-я степень: тоник
- 2-я степень: супертоник
- 3-я степень: медиант
- 4-я степень: субдоминанта
- 5-я степень: доминант
- 6-я степень: субмедиант
- 7-я ступень: ведущая нота (или ведущий тон)
8-я ступень звукоряда фактически является тоникой, но на октаву выше.
По этой причине, называя градусы шкалы, вы всегда должны называть их 1-й степенью.
Для получения дополнительной информации ознакомьтесь с моим подробным руководством по именам степеней шкалы здесь.
Крупные шкалы
Одним из наиболее распространенных типов шкал является основная шкала .
Мажорные гаммы определяются сочетанием полутонов и тонов (целые шаги и полутоны):
Тон — Тон — Полутон — Тон — Тон — Тон — Полутон
Или целыми шагами и полушагами:
Целый — Целый — Половина — Целый — Целый — Целый — Половина
Формула основной шкалы G major scaleВы можете использовать эту формулу целых шагов и полушагов, чтобы сформировать мажорную гамму, начиная с любой ноты.
Для более глубокого изучения формирования основных шкал ознакомьтесь с этим постом, в котором мы рассмотрим все 12 основных шкал.
Мелкая шкала
Второй тип шкалы, который мы собираемся рассмотреть, — это малая шкала .
Минорные гаммы также имеют семь нот, как и мажорная гамма, но они определяются наличием сглаженной трети.
Это означает, что третья нота шкалы находится на три полутона выше первой ноты, в отличие от мажорных гамм, где третья нота шкалы находится на четыре полутона выше.
Мелодическая минорная гаммаСуществует три различных типа минорной гаммы:
Каждый тип минорной гаммы использует немного разную формулу полутонов и тонов, но все они имеют минорную треть.
Подробнее о типах минорных гамм читайте в моем посте здесь.
Мажорные клавиши довольно часто ассоциируются с музыкой, дающей ощущение счастья или радости, тогда как второстепенные клавиши известны музыкой, которая звучит грустно или меланхолично.
Вот видео для демонстрации Прелюдии ми минор Шопена.
Прелюдия Шопена ми минорХроматические гаммы
Две гаммы, которые мы рассмотрели до сих пор, называются диатоническими.
Это означает, что они находятся в «тональности», и первая нота гаммы — тоника.
Диатонические гаммы также являются гептоническими (что означает, что они имеют семь нот) с двумя интервалами полутона (полутона) и пятью интервалами, которые являются тонами (целые шаги).
Хроматическая гамма сильно отличается от диатонической гаммы, поскольку она состоит из всех 12 нот западной музыки.
Каждая нота хроматической гаммы представляет собой интервал полутона (полутона) отдельно от других. Другими словами, чтобы сыграть хроматическую гамму, вы выбираете ноту, затем играете ноту на полтона выше и продолжаете играть, пока не дойдете до ноты, с которой начали.
Например, это восходящая хроматическая шкала, начинающаяся с C:
. Восходящая хроматическая шкала на C Хроматическая шкала, начиная с CА вот нисходящая хроматическая шкала, начиная с Gb:
Нисходящая хроматическая гамма на G-бемолеПоскольку хроматические гаммы используют каждую отдельную ноту, мы не говорим, что хроматическая гамма находится в определенной тональности.Мы просто используем ноту, с которой начинается шкала.
Чтобы узнать больше, ознакомьтесь с моим руководством по хроматическим гаммам здесь.
Целые тональные шкалы
Целый тон Шкала — это тип шкалы, в которой каждая нота представляет собой интервал тона (целый шаг).
Это полная противоположность хроматической гамме, где каждая нота находится на расстоянии полутона друг от друга.
Целый тон — это разновидность гексатонической гаммы, что означает, что в нем всего шесть нот.
Это потому, что на всей шкале тонов нет полутонов (полутонов).
Целая шкала тонов, начиная с CЦелая шкала тонов имеет очень характерный звук, и с ними можно весело поиграть.
Чтобы узнать о них больше, я написал более подробный пост о целых шкалах тонов здесь.
Шкала пентатоники
Следующий тип шкалы, который мы собираемся рассмотреть, — это шкала пентатоники .
Пентатонические гаммы — одни из самых простых и существуют уже очень давно.
Считается, что им может быть даже 50 000 лет!
Слово пентатоника происходит от греческого слова «пенте», означающего пять.
Это то же греческое слово, от которого мы получили «пятиугольник», означающий пятиугольную форму.
Пять нот в мажорной пентатонике:
- Первая ступень — тоническая
- Вторая ступень — супертоническая
- Третья ступень — медиант
- Пятая ступень — доминантная
- Шестая ступень — субмедиант
Вот пентатоническая шкала до мажор, так что вы можете видеть:
Пентатоника до мажорПентатоника очень распространена во многих музыкальных произведениях, с которыми вы будете знакомы: от блюза и джаза до фолка и рок-музыки, простота пентатоники делает ее очень универсальной.

 По результатам такой проверки можно дополнительно вычислять частоты заполнения (вероятности) для различных классов, которые могут использоваться для применения различных методов статистического анализа[5] — критерия согласия Хи-квадрат, критерия Крамера для проверки гипотезы о связи качественных признаков и др.
По результатам такой проверки можно дополнительно вычислять частоты заполнения (вероятности) для различных классов, которые могут использоваться для применения различных методов статистического анализа[5] — критерия согласия Хи-квадрат, критерия Крамера для проверки гипотезы о связи качественных признаков и др. Определение нулевой точки — сложная задача для психологических исследований, накладывающая ограничение на использование данной шкалы. С помощью таких шкал могут быть измерены масса, длина, сила, стоимость (цена). Пример: шкала Кельвина (температур, отсчитанных от абсолютного нуля, с выбранной по соглашению специалистов единицей измерения — Кельвин).
Определение нулевой точки — сложная задача для психологических исследований, накладывающая ограничение на использование данной шкалы. С помощью таких шкал могут быть измерены масса, длина, сила, стоимость (цена). Пример: шкала Кельвина (температур, отсчитанных от абсолютного нуля, с выбранной по соглашению специалистов единицей измерения — Кельвин).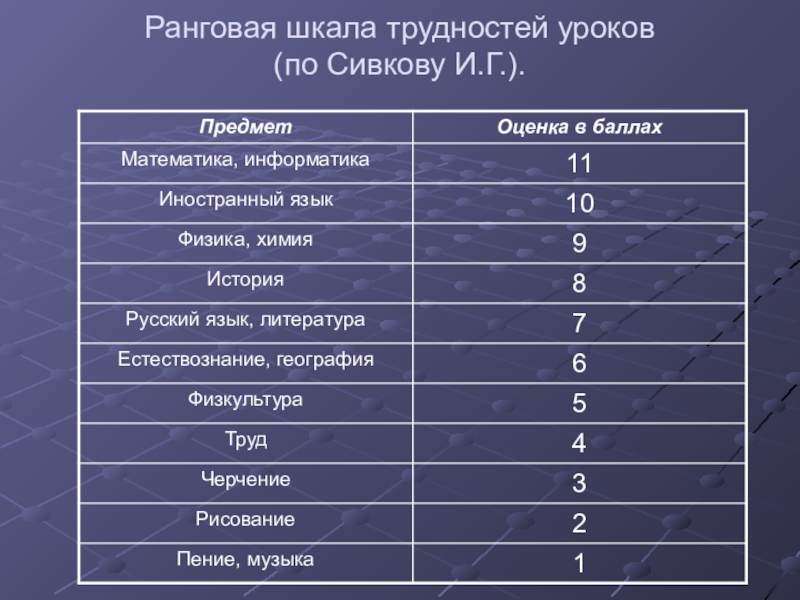 Пропустите этот шаг, если вас не интересуют ноты музыкальной гаммы и вы просто хотите получить полутоновый узор.
Пропустите этот шаг, если вас не интересуют ноты музыкальной гаммы и вы просто хотите получить полутоновый узор.